Question

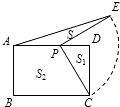在矩形ABCD中，AD=4，点P在AD上，且AP：PD=a：b
（1）求△PCD的面积S₁与梯形ABCP的面积S₂的比值（用含a，b的代数式表示）；
（2）将线段PC绕点P逆时针旋转90°至PE，求△APE的面积S（用含a，b的代数式表示）．

Answer 1

解：（1），，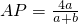
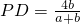设AB=h，则S₁=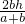，S₂=.．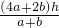
∴．

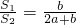（2）过E作AD的垂线交AD（或AD的延长线）于点F，过P作BC的垂线交BC于点G．
在Rt△PFE和Rt△PGC中，
PE=PC，∠EPF=∠CPG，∴△PFE≌△PGC，
∴EF=GC=PD=．
∴．
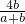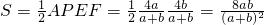分析：（1）AP：PD=a：b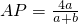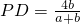，，，设AB=h，则可表示出△PCD的面积S₁与梯形ABCP的面积S₂从而可得出答案；
（2）过E作AD的垂线交AD（或AD的延长线）于点F，过P作BC的垂线交BC于点G，证明△PFE≌△PGC即可求解；
点评：本题考查了梯形，难度适中，主要是过E作AD的垂线交AD（或AD的延长线）于点F，过P作BC的垂线交BC于点G．