题目内容
 已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°.
已知直线AB和CD相交于O点,射线OE⊥AB于O,射线OF⊥CD于O,且∠BOF=25°.求:∠AOC与∠EOD的度数.
考点:对顶角、邻补角,垂线
专题:
分析:由OE⊥AB,得∠COE=90°,由OF⊥CD,得∠COF=90°,再结合角平分线和对顶角的性质得到答案.
解答:解:∵OF⊥CD,∴∠DOF=90°,
又∵∠BOF=25°,
∴∠BOD=90°+25°=115°,
∴∠AOC=∠BOD=115°,
由OE⊥AB,得∠COE=90°,
又∵∠BOF=25°,∴∠EOF=65°,
∴∠EOD=∠DOF-∠EOF=25°.
又∵∠BOF=25°,
∴∠BOD=90°+25°=115°,
∴∠AOC=∠BOD=115°,
由OE⊥AB,得∠COE=90°,
又∵∠BOF=25°,∴∠EOF=65°,
∴∠EOD=∠DOF-∠EOF=25°.
点评:此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线、角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
相关题目
 如图是小明画出的雨季某地某星期降雨量的条形图.
如图是小明画出的雨季某地某星期降雨量的条形图.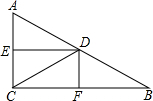 已知,如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形.
已知,如图,在△ABC中,∠ACB=90°,D是AB的中点,DE、DF分别是△BDC、△ADC的角平分线.求证:四边形DECF是矩形.