题目内容
若⊙O1的半径为1,⊙O2的半径为2,且O1O2的长是一元二次方程x(x-3)=x-3的一个实数根,则⊙O1和⊙O2的位置关系为
- A.内切
- B.外切
- C.相切
- D.内含
C
分析:解答此题,先要求一元二次方程的两根,然后根据圆与圆的位置关系判断条件,确定位置关系.
解答:一元二次方程x(x-3)=x-3化成一般形式,
x2-4x+3=0,
∵O1O2的长是一元二次方程x(x-3)=x-3的一个实数根,
∴O1O2=1或3,
当O1O2=1,两圆内切,
O1O2=3,两圆外切.
故两圆相切.
故选C.
点评:主要是考查解一元二次方程,圆与圆的位置关系与数量关系间的联系.
分析:解答此题,先要求一元二次方程的两根,然后根据圆与圆的位置关系判断条件,确定位置关系.
解答:一元二次方程x(x-3)=x-3化成一般形式,
x2-4x+3=0,
∵O1O2的长是一元二次方程x(x-3)=x-3的一个实数根,
∴O1O2=1或3,
当O1O2=1,两圆内切,
O1O2=3,两圆外切.
故两圆相切.
故选C.
点评:主要是考查解一元二次方程,圆与圆的位置关系与数量关系间的联系.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 11、如图,若⊙O1的半径为10,⊙O2的半径为5,圆心距是13,则两圆的外公切线AB长是
11、如图,若⊙O1的半径为10,⊙O2的半径为5,圆心距是13,则两圆的外公切线AB长是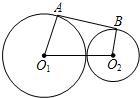 23、如图,若⊙O1的半径为11cm,⊙O2的半径为6cm,圆心距是13cm,则两圆的公切线长是
23、如图,若⊙O1的半径为11cm,⊙O2的半径为6cm,圆心距是13cm,则两圆的公切线长是 如图,AB是⊙O1的直径,AO1是⊙O2的直径,弦MN∥AB,且MN与⊙O2相切于点C,若⊙O1的半径为2.求:阴影部分的面积.
如图,AB是⊙O1的直径,AO1是⊙O2的直径,弦MN∥AB,且MN与⊙O2相切于点C,若⊙O1的半径为2.求:阴影部分的面积. 如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直线的半圆O1与以BC为直径的半圆O2相切于点D.
如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直线的半圆O1与以BC为直径的半圆O2相切于点D.