Question

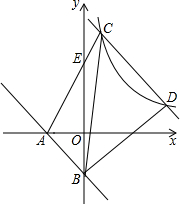如图，直线l：y=-2x-2，与x轴y轴交于A，B两点，平移直线l交双曲线y=

k

x

（x＞0）于C，D两点，且CD=2AB，连接AC，交y轴于E点，S_△ABC=3S_△ABE，求k的值．

Answer 1

考点：反比例函数综合题

专题：

分析：先由直线l：y=-2x-2与x轴、y轴交于A，B两点，求出A（-1，0），B（0，-2），利用两点之间的距离公式得到AB²=1+4=5，由CD=2AB，得出CD²=4AB²=20．再由S_△ABC=3S_△ABE，S_△ABC=S_△BCE+S_△ABE，得出S_△BCE=2S_△ABE，根据同底的两个三角形面积之比等于高之比得到C点横坐标为2．再设直线CD的解析式为y=-2x+b，那么C（2，b-4）．为求D点坐标，把y=-2x+b代入y=

k

x

，整理得2x²-bx+k=0，解得x=

b± b2-8k

4

，由

b- b2-8k

4

=2，得

b2-8k

=b-8，所以

b+ b2-8k

4

=

b+b-8

4

=

b-4

2

，于是D（

b-4

2

，4），CD²=（

b-4

2

-2）²+（b-4-4）²=

5

4

（b-8）²=20，解方程求出b的值，那么k=2（b-4），代入计算即可．

解答：解：∵直线l：y=-2x-2与x轴y轴交于A，B两点，
∴当x=0时，y=-2；y=0时，-2x-2=0，x=-1；
∴A（-1，0），B（0，-2），
∴AB²=1+4=5，
∵CD=2AB，
∴CD²=4AB²=20．
∵S_△ABC=3S_△ABE，S_△ABC=S_△BCE+S_△ABE，
∴S_△BCE=2S_△ABE，
∴C点横坐标为2．
设直线CD的解析式为y=-2x+b，则C（2，b-4）．
把y=-2x+b代入y=

k

x

，得-2x+b=

k

x

，
整理得2x²-bx+k=0，
解得x=

b± b2-8k

4

，
∵

b- b2-8k

4

=2，
∴

b2-8k

=b-8，
∴

b+ b2-8k

4

=

b+b-8

4

=

b-4

2

，
当x=

b-4

2

时，y=-2×

b-4

2

+b=4，
∴D（

b-4

2

，4），
∴CD²=（

b-4

2

-2）²+（b-4-4）²=

5

4

（b-8）²=20，
解得b₁=12，b₂=4（不合题意舍去），
∴k=2（b-4）=2×（12-4）=16．
故答案为16．

点评：本题是反比例函数综合题，其中涉及两点之间的距离公式，三角形面积，待定系数法，公式法解一元二次方程，坐标轴上点的坐标特征等知识点，综合性较强，有一定的难度．