Question

【题目】已知抛物线l1：y=﹣x2+2x+3与x轴交于点A，B（点A在点B左边），与y轴交于点C，抛物线l2经过点A，与x轴的另一个交点为E（4，0），与y轴交于点D（0，﹣2）．

（1）求抛物线l2的解析式；
（2）点P为线段AB上一动点（不与A、B重合），过点P作y轴的平行线交抛物线l1于点M，交抛物线l2于点N．
①当四边形AMBN的面积最大时，求点P的坐标；
②当CM=DN≠0时，求点P的坐标．

Answer 1

【答案】
（1）解：∵令﹣x2+2x+3=0，解得：x1=﹣1，x2=3，

∴A（﹣1，0），B（3，0）．

设抛物线l2的解析式为y=a（x+1）（x﹣4）．

∵将D（0，﹣2）代入得：﹣4a=﹣2，

∴a= ．

∴抛物线的解析式为y= x2﹣ x﹣2

（2）解：①如图1所示：

∵A（﹣1，0），B（3，0），

∴AB=4．

设P（x，0），则M（x，﹣x2+2x+3），N（x， x2﹣ x﹣2）．

∵MN⊥AB，

∴SAMBN= ABMN=﹣3x2+7x+10（﹣1＜x＜3）．

∴当x= 时，SAMBN有最大值．

∴此时P的坐标为（ ，0）．

②如图2所示：作CG⊥MN于G，DH⊥MN于H，如果CM与DN不平行．

∵DC∥MN，CM=DN，

∴四边形CDNM为等腰梯形．

∴∠DNH=∠CMG．

在△CGM和△DNH中 ，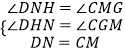

∴△CGM≌△DNH．

∴MG=HN．

∴PM﹣PN=1．

设P（x，0），则M（x，﹣x2+2x+3），N（x， x2﹣ x﹣2）．

∴（﹣x2+2x+3）+（ x2﹣ x﹣2）=1，解得：x1=0（舍去），x2=1．

∴P（1，0）．

当CM∥DN时，如图3所示：

∵DC∥MN，CM∥DN，

∴四边形CDNM为平行四边形．

∴DC=MN．=5

∴﹣x2+2x+3﹣（ x2﹣ x﹣2）=5，

∴x1=0（舍去），x2= ，

∴P（ ，0）．

总上所述P点坐标为（1，0），或（ ，0）．

【解析】1、直线l2经过A、D、E三点，只需求出A点坐标，就可以求出直线l2的解析式；2、①四边形AMBN的对角线互相垂直，SAMBN= ABMN，由A、B两点坐标求出线段AB的长，MN⊥AB得出点P、M、N三点的横坐标相同，设P（x，0），可以表示出点M、N的坐标，从而列出s与x的函数关系式，求得s的最大值时，x的值，于是就可以求得点P的坐标；②当CM=DN≠0时，分两种情况，当CM∥DN时四边形CDNM为平行四边形；当CM不平行 DN时，四边形CDNM为等腰梯形．就可以求出点P的坐标。