��Ŀ����
����Ŀ�����Ƕ��壺����������ϵ��֮��Ϊ1���Գ�����ͬ����ͼ����y�ύ��Ҳ��ͬ�Ķ��κ�����Ϊ�Ѻ�ͬ����κ��������磺y��2x2+4x��5���Ѻ�ͬ����κ���Ϊy����x2��2x��5��
��1������д��y��![]() x2+x��5���Ѻ�ͬ����κ�����
x2+x��5���Ѻ�ͬ����κ�����
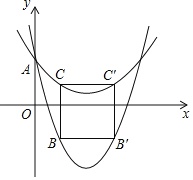
��2����ͼ�����κ���L1��y��ax2��4ax+1�����Ѻ�ͬ����κ���L2����y�ύ�ڵ�A����B��C�ֱ���L1��L2�ϣ���B��C�ĺ������Ϊm��0��m��2�����ǹ���L1�ĶԳ���ĶԳƵ�ֱ�ΪB����C��������BB����B��C����C��C��CB����a��3�����ı���BB��C��CΪ�����Σ���m��ֵ��
���𰸡���1��y��![]() x2+2x��5����2��
x2+2x��5����2��![]()
��������
��1�������Ѻ�ͬ����κ����Ķ���������ɣ�
��2���ȸ��ݶ��κ���L1�Ľ���ʽ�ó����Ѻ�ͬ����κ���L2�ĺ�������ʽ������a��3�����ö��κ���ͼ���ϵ�����������ɵó���B��C��B����C�������꣬�����ɵó�BC��BB����ֵ���������ε����ʿɵ�BC��BB�������ɵó�����m��һԪ���η��̣���֮ȡ�����0С��2��ֵ���ý����
�⣺��1����![]() ��1����
��1����![]() ����2��
����2��
�ຯ��y��![]() x2+x��5���Ѻ�ͬ����κ���Ϊy��
x2+x��5���Ѻ�ͬ����κ���Ϊy��![]() x2+2x��5��
x2+2x��5��
��2�����κ���L1��y��ax2��4ax+1�ĶԳ���Ϊֱ��x����![]() ��2�����Ѻ�ͬ����κ���L2��y����1��a��x2��4��1��a��x+1��
��2�����Ѻ�ͬ����κ���L2��y����1��a��x2��4��1��a��x+1��
��a��3��
������L1��y��ax2��4ax+1��3x2��12x+1�������L2��y����1��a��x2��4��1��a��x+1����2x2+8x+1��
���B��������m��3m2��12m+1������C��������m����2m2+8m+1����
���B����������4��m��3m2��12m+1������C����������4��m����2m2+8m+1����
��BC����2m2+8m+1����3m2��12m+1������5m2+20m��BB����4��m��m��4��2m��
���ı���BB��C��CΪ�����Σ�
��BC��BB��������5m2+20m��4��2m��
��ã�m1��![]() ��m2��
��m2��![]() ���������⣬��ȥ����
���������⣬��ȥ����
��m��ֵΪ![]() ��
��