题目内容
⊙O的半径为3cm，直线EF切⊙O于点B，点A，C在直线EF上，且AB=3cm，BC=| 3 |
分析：本题要分两种情况讨论：
（1）当A，C在B的两侧时，连接OB，利用直角三角形中的三角函数值可求得对应的角的度数．
（2）当A，C在B的同侧时，连接OB，利用直线EF切⊙O于点B构造直角三角形，利用三角函数值可求得对应的角的度数，即可求解．
（1）当A，C在B的两侧时，连接OB，利用直角三角形中的三角函数值可求得对应的角的度数．
（2）当A，C在B的同侧时，连接OB，利用直线EF切⊙O于点B构造直角三角形，利用三角函数值可求得对应的角的度数，即可求解．
解答：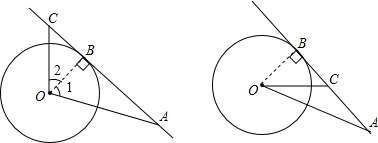
解：如图：本题要分两种情况讨论：
当A，C在B的两侧时如图（一）
连接OB．
∵直线EF切⊙O于点B，
∴OB⊥AC，OB=3cm，tan∠1=
=
=1，tan∠2=
=
．
∴∠1=45°，∠2=30°．
∴∠AOC=∠1+∠2=45°+30°=75°．
当A，C在B的同侧时如图（二）
连接OB．
∵直线EF切⊙O于点B，
∴OB⊥AC，OB=3cm．
∴tan∠AOB=
=
=1，tan∠2=
=
．
∴∠AOB=45°，∠BOC=30°．
∴∠AOC=∠AOB-∠BOC=45°-30°=15°．
故∠AOC=75°或15°．
故答案为：75°或15°．
解：如图：本题要分两种情况讨论：当A，C在B的两侧时如图（一）
连接OB．
∵直线EF切⊙O于点B，
∴OB⊥AC，OB=3cm，tan∠1=
| AB |
| OB |
| 3 |
| 3 |
| BC |
| OB |
| ||
| 3 |
∴∠1=45°，∠2=30°．
∴∠AOC=∠1+∠2=45°+30°=75°．
当A，C在B的同侧时如图（二）
连接OB．
∵直线EF切⊙O于点B，
∴OB⊥AC，OB=3cm．
∴tan∠AOB=
| AB |
| OB |
| 3 |
| 3 |
| BC |
| OB |
| ||
| 3 |
∴∠AOB=45°，∠BOC=30°．
∴∠AOC=∠AOB-∠BOC=45°-30°=15°．
故∠AOC=75°或15°．
故答案为：75°或15°．
点评：此题属中等难度题，解答此题的关键是时要熟知特殊角的三角函数值，在解答时要注意分类讨论，不要漏解．
练习册系列答案
相关题目
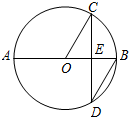如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，⊙O的半径为| 3 |
A、
| ||
| B、3cm | ||
C、2
| ||
| D、9cm |