题目内容
如图，AB是⊙O的弦，点C、D在弦AB上，且OC=OD．求证：AC=BD．
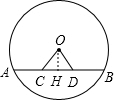证明：过点O作OH⊥AB，垂足为H，（1分）∴AH=BH，（2分）
∵OC=OD，且OH⊥CD，
∴CH=DH，（4分）
∴AH-CH=BH-DH，
∴AC=BD．（6分）
分析：过点O作OH⊥AB，垂足为H，由垂径定理可知AH=BH，再由OC=OD可判断出△OAD是等腰三角形，由等腰三角形的性质可知CH=DH，进而可求出答案．
点评：本题考查的是垂径定理及等腰三角形的判定及性质，根据题意作出辅助线是解答此题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
5、已知：如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB=8m，OC=5m，则DC的长为（ ）
如图，AB是⊙O的弦，⊙O半径为5，OC⊥AB于D，交⊙O于C，且CD=2，则AB=
14、已知：如图，AB是⊙O的弦，半径OC交弦AB于点P，且AB=10cm，PB=4cm，PC=2cm，则OC的长等于
如图，AB是⊙O的弦，AB=10，⊙O的半径OC⊥AB于D，如果OD：DC=3：2，那么⊙O的直径长为
如图，AB是⊙O的弦，OC⊥AB于点C，若AB=4，OC=1，则⊙O的半径为（ ）