Question

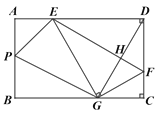
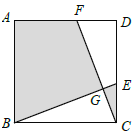
【题目】如图，在正方形中，，点分别在、上，，相交于. 若图中阴影部分的面积与正方形的面积之比为，则的周长为______.

Answer 1

【答案】

【解析】

根据阴影部分的面积与正方形ABCD的面积之比为2：3，得出阴影部分的面积为24，空白部分的面积为12，进而依据△BCG的面积以及勾股定理，得出BG+CG的长，进而得出其周长．

解：∵阴影部分的面积与正方形ABCD的面积之比为2：3，

∴阴影部分的面积为

∴空白部分的面积为36-24=12，

由CE=DF，BC=CD，∠BCE=∠CDF=90°，可得△BCE≌△CDF，

∴△BCG的面积与四边形DEGF的面积相等，均为 ，

∠CBE=∠DCF，

∵∠DCF+∠BCG=90°，

∴∠CBG+∠BCG=90°，即∠BGC=90°，

设BG=a，CG=b，则，

又∵a2+b2=62，

∴a2+2ab+b2=36+24=60，

即（a+b）2=60，

∴a+b=，即BG+CG=，

∴△BCG的周长=

故答案为：．