Question

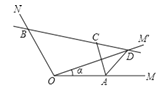
【题目】如图，已知∠MON＝120°，点A，B分别在OM，ON上，且OA＝OB＝a，将射线OM绕点O逆时针旋转得到OM′，旋转角为α（0°＜α＜120°且α≠60°），作点A关于直线OM′的对称点C，画直线BC交OM′于点D，连接AC，AD，则有：(1)AD＝__ CD(填数量关系)；(2)△ACD面积的最大值为_____．

Answer 1

【答案】1

【解析】

(1) 根据对称的性质：对称点的连线被对称轴垂直平分可得：OM'是AC的垂直平分线，再由垂直平分线的性质可作判断；(2) 作⊙O，根据四点共圆的性质得：∠ACD=∠E=60°，证明△ACD是等边三角形，当AC最大时，△ACD的面积最大，当AC为直径时最大，根据面积公式计算后可作判断．

(1)∵A、C关于直线OM′对称，

∴OM′是AC的垂直平分线，

∴AD=1CD；

(2) 连接OC，

由(1)知：OM′是AC的垂直平分线，

∴OC=OA，

∴OA=OB=OC，

以O为圆心，以OA为半径作⊙O，交AO的延长线于E，连接BE，则A、B、C都在⊙O上，

∵∠MON=120°，

∴∠BOE=60°，

∵OB=OE，

∴△OBE是等边三角形，

∴∠E=60°，

∵A、C、B、E四点共圆，

∴∠ACD=∠E=60°，

∵CD=AD，∠ACD=60°，

∴△ACD是等边三角形，

当AC最大时，△ACD的面积最大，

∵AC是⊙O的弦，即当AC为直径时最大，此时AC=2OA=2a，α=90°，

∴△ACD面积的最大值是：.