题目内容
平面上有四个点(没有三点共线),以这四个点为顶点作三角形,其中锐角三角形最多有( )个.
| A、3 | B、2 | C、1 | D、0 |
考点:三角形边角关系
专题:
分析:平面内的四个点(没有三点共线)可以组成4个三角形.假设以每三个点为顶点的三角形都是锐角三角形,记四个点为A、B、C、D,考虑点D在△ABC之内与之外这两种情况,利用与已知定理矛盾,从而假设不成立.以此推断其中锐角三角形最多有3个.
解答: 解:平面内的四个点(没有三点共线)可以组成4个三角形.
解:平面内的四个点(没有三点共线)可以组成4个三角形.
假设以每三个点为顶点的三角形都是锐角三角形,记四个点为A、B、C、D,考虑点D在△ABC之内与之外这两种情况.
(1)如果点D在△ABC之内,由假设知围绕点D的三个角都是锐角,其和小于270°,这与一个周角等于360°相矛盾,根据∠ADB、∠BDC、∠ADC三个角一定小于180°,即其中两个的和一定大于180°,则三个角中最多有2个锐角,即△ABD、△ADC和△BDC中最多有2个锐角三角形,加上△ABC,则图中最多有3个锐角三角形.
(2)如果点D在△ABC之外,由假设知∠ABC、∠BCD、∠CDA、∠DAB都小于90°,这与四边形的内角和为360°相矛盾,则四个角中最多有3个锐角,则四个三角形中最多有三个锐角三角形.
综上所述,锐角三角形最多有3个.
故选A.
 解:平面内的四个点(没有三点共线)可以组成4个三角形.
解:平面内的四个点(没有三点共线)可以组成4个三角形.假设以每三个点为顶点的三角形都是锐角三角形,记四个点为A、B、C、D,考虑点D在△ABC之内与之外这两种情况.
(1)如果点D在△ABC之内,由假设知围绕点D的三个角都是锐角,其和小于270°,这与一个周角等于360°相矛盾,根据∠ADB、∠BDC、∠ADC三个角一定小于180°,即其中两个的和一定大于180°,则三个角中最多有2个锐角,即△ABD、△ADC和△BDC中最多有2个锐角三角形,加上△ABC,则图中最多有3个锐角三角形.
(2)如果点D在△ABC之外,由假设知∠ABC、∠BCD、∠CDA、∠DAB都小于90°,这与四边形的内角和为360°相矛盾,则四个角中最多有3个锐角,则四个三角形中最多有三个锐角三角形.
综上所述,锐角三角形最多有3个.
故选A.
点评:本题考查了三角形的内角和定理,正确判断∠ADB、∠BDC、∠ADC三个角中最多有2个锐角,以及∠ABC、∠BCD、∠CDA、∠DAB四个三角形中最多有三个锐角三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=x2+2x-2写成y=a(x-h)2+k的形式是( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2-3 |
| C、y=(x-1)2+1 |
| D、y=(x+2)2-1 |
 如图所示,两个全等的等边三角形的边长1m,一个微型机器人由A点开始按A-B-C-D-B-E-A的顺序沿等边三角形的边循环运动,行走2014m停下,则这个微型机器人停在( )
如图所示,两个全等的等边三角形的边长1m,一个微型机器人由A点开始按A-B-C-D-B-E-A的顺序沿等边三角形的边循环运动,行走2014m停下,则这个微型机器人停在( )| A、点A处 | B、点B处 |
| C、点C处 | D、点E处 |
若
=2-a,则a与2的关系是( )
| 4-4a+a2 |
| A、a<2 | B、a≤2 |
| C、a>2 | D、a≥2 |
2014年3月5日,国务院总理李克强作政府工作报告时表示,2013年经济运行稳中向好,国内生产总值达到56.9万亿元,比上年增长7.7%.用科学记数法表示56.9万亿元为( )
| A、5.69×104亿元 |
| B、5.69×105亿元 |
| C、56.9×104亿元 |
| D、0.569×106亿元 |
用科学记数方法表示-0.0000907,得( )
| A、9.07×10-4 |
| B、9.07×10-5 |
| C、9.07×105 |
| D、-9.07×10-5 |
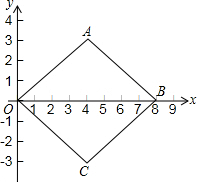 如图1,在平面直角坐标系xOy中,菱形OABC的顶点O与坐标原点重合,点A的坐标为A(4,3),点B在x轴的正半轴上.
如图1,在平面直角坐标系xOy中,菱形OABC的顶点O与坐标原点重合,点A的坐标为A(4,3),点B在x轴的正半轴上.