题目内容
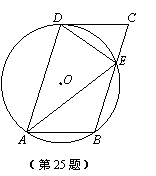
如图,在□ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
(1)判断四边形ABED的形状,并说明理由;
(2)判断直线DC与⊙O的位置关系,并说明理由;
(3)若AB=3,AE=6,求CE的长.
 |

(1)四边形ABED是等腰梯形.
理由如下:在□ABCD中,AD∥BC,
∴∠DAE=∠AEB.
∴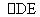 =
=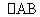 ,DE=AB.
,DE=AB.
∵AB∥CD,∴A B与DE不平行.
B与DE不平行.
∴四边形ABDE是等腰梯形.
 (2)直线DC与⊙O相切.
(2)直线DC与⊙O相切.
如图,作直径 DF,连接AF.
DF,连接AF.
于是,∠EAF=∠EDF.
∵∠DAE=∠CDE,
∴∠EAF+∠DAE=∠EDF+∠CDE,即∠DAF=∠CDF.
∵DF是⊙O的直径,点A在⊙O上,
∴∠DAF=90°,∴∠CDF=90°.∴OD⊥CD.
直线DC经过⊙O半径OD外端D,且与半径垂直,
直线DC与⊙O相切.
(3)由(1),∠EDA=∠DAB.
在□ABCD中,∠DAB=∠DCB,
∴∠EDA=∠DCB.又∵∠DAE=∠CDE,∴△ADE∽△DCE.∴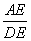 =
=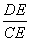 ,
,
∵AB=3,由(1)得,AB=DE=DC=3.即  =
= .
.
解得,CE= .
.

练习册系列答案
相关题目
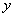 (km)与所用时间
(km)与所用时间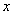 ( h)的函数关系图象;
( h)的函数关系图象;

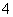 和
和 ,则此三角形的第三边长可以是( )
,则此三角形的第三边长可以是( ) C.
C.
 ,那么这个多边形的边数是 .
,那么这个多边形的边数是 .
 H370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为_____
H370失联事件发生后第30天,中国“海巡01”轮在南印度洋海域搜索过程中首次侦听到疑是飞机黑匣子的脉冲信号,探测到的信号所在海域水深4500米左右,其中4500用科学记数法表示为_____