题目内容
如图,▱ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
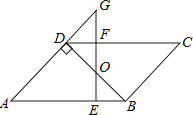
(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中

∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG= =DO,
=DO,
∴在等腰RT△ADB 中,DB=2DO=2 =AD
=AD
∴AD=2 ,
,


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列计算正确的是( )
|
| A. | a2•a3=a6 | B. | (﹣2ab)2=4a2b2 |
|
| C. | (a2)3=a5 | D. | 3a2b2÷a2b2=3ab |
下列关于二次函数y=ax2﹣2ax+1(a>1)的图象与x轴交点的判断,正确的是( )
|
| A. | 没有交点 |
|
| B. | 只有一个交点,且它位于y轴右侧 |
|
| C. | 有两个交点,且它们均位于y轴左侧 |
|
| D. | 有两个交点,且它们均位于y轴右侧 |



 B、
B、 C、
C、 D、
D、