题目内容
如图，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，使点B与点A重合，折痕为DE，则△ACD的周长为
- A.10cm
- B.12cm
- C.15cm
- D.20cm
C
分析：根据图形反折变换的性质得出AD=BD，故AC+（CD+AD）=AC+BC，由此即可得出结论．
解答：∵△ADE由△BDE反折而成，AC=5cm，BC=10cm，
∴AD=BD，
∴△ACD的周长=AC+CD+AD=AC+BC=15cm．
故选C．
点评：本题考查的是翻折变换，熟知图形反折不变性的性质是解答此题的关键．
分析：根据图形反折变换的性质得出AD=BD，故AC+（CD+AD）=AC+BC，由此即可得出结论．
解答：∵△ADE由△BDE反折而成，AC=5cm，BC=10cm，
∴AD=BD，
∴△ACD的周长=AC+CD+AD=AC+BC=15cm．
故选C．
点评：本题考查的是翻折变换，熟知图形反折不变性的性质是解答此题的关键．
练习册系列答案
特高级教师点拨系列答案
文敬图书课时先锋系列答案
相关题目
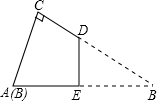如图，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，点B与点A重合，折痕为DE，则CD的长为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，点B与点A重合，折痕为DE，则CD的长为
如图，有一张直角三角形纸片，两直角边AC=6 cm，BC=8cm，D是BC上一点，AD=DB，DE⊥AB，垂足为E，CD等于（ ）cm．A、
| ||
B、
| ||
C、
| ||
D、
|
如图，有一张直角三角形纸片，两直角边AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE，求CD的长．
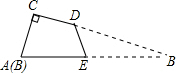如图，有一张直角三角形纸片，两直角边AC=6cm，BC=9cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于（ ）cm．A、
| ||
B、
| ||
C、
| ||
D、
|