题目内容
一次函数y=kx+1-k的图象与函数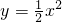 的图象有________个交点.
的图象有________个交点.
二
分析:先由两解析式组成方程组,消去y得到关于x的方程 x2-kx+k-1=0,再计算△=k2-4×
x2-kx+k-1=0,再计算△=k2-4× (k-1)=k2-2k+2=(k-1)2+1,可得到△>0,于是关于x的方程有两个不相等的实数解,所以
(k-1)=k2-2k+2=(k-1)2+1,可得到△>0,于是关于x的方程有两个不相等的实数解,所以
一次函数与二次函数的图象有两个交点.
解答:对于方程组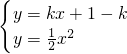 消去y得kx+1-k=
消去y得kx+1-k= x2,
x2,
整理得 x2-kx+k-1=0,
x2-kx+k-1=0,
△=k2-4× (k-1)=k2-2k+2=(k-1)2+1,
(k-1)=k2-2k+2=(k-1)2+1,
∵(k-1)2+1≥0,
∴(k-1)2+1>0,即△>0,
∴关于x的方程有两个不相等的实数解,
∴方程组有两组解,即一次函数与二次函数的图象有两个交点.
故答案为二
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=- ;抛物线与y轴的交点坐标为(0,c).也考查了一次函数的性质以及函数图象的交点问题.
;抛物线与y轴的交点坐标为(0,c).也考查了一次函数的性质以及函数图象的交点问题.
分析:先由两解析式组成方程组,消去y得到关于x的方程
 x2-kx+k-1=0,再计算△=k2-4×
x2-kx+k-1=0,再计算△=k2-4× (k-1)=k2-2k+2=(k-1)2+1,可得到△>0,于是关于x的方程有两个不相等的实数解,所以
(k-1)=k2-2k+2=(k-1)2+1,可得到△>0,于是关于x的方程有两个不相等的实数解,所以一次函数与二次函数的图象有两个交点.
解答:对于方程组
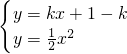 消去y得kx+1-k=
消去y得kx+1-k= x2,
x2,整理得
 x2-kx+k-1=0,
x2-kx+k-1=0,△=k2-4×
 (k-1)=k2-2k+2=(k-1)2+1,
(k-1)=k2-2k+2=(k-1)2+1,∵(k-1)2+1≥0,
∴(k-1)2+1>0,即△>0,
∴关于x的方程有两个不相等的实数解,
∴方程组有两组解,即一次函数与二次函数的图象有两个交点.
故答案为二
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
 ;抛物线与y轴的交点坐标为(0,c).也考查了一次函数的性质以及函数图象的交点问题.
;抛物线与y轴的交点坐标为(0,c).也考查了一次函数的性质以及函数图象的交点问题. 
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
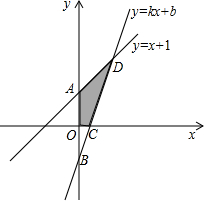 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D.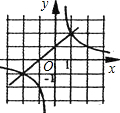 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y= (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,