题目内容
将边长为6的正方形纸片ABCD的顶点A沿折痕EF(E在AB上,F在CD上)折叠,A恰好与BC的一个三等分点G(靠近B侧)重合,
则EF=________.
2
分析:先根据题意画出图形,连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,再利用勾股定理求出AE的长,设DF=y,则CF=6-y,CG=4,再由等腰三角形的性质及勾股定理可求出EH、FH的值,进而可求出答案.
解答: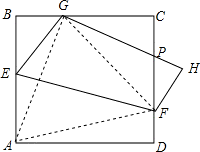 解:连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,
解:连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,
设AE=GE=x,则BE=6-x,BG=2,
在Rt△BEG中,由勾股定理得EG2=BE2+BG2,
即x2=(6-x)2+22,
解得x= ,
,
设DF=y,则CF=6-y,CG=4,在Rt△ADF中,
AF2=AD2+DF2,即AF2=36+y2,
在Rt△CGF中,GF2=CG2+CF2,
由勾股定理得,
36+y2=(6-y)2+16,
解得y= ,
,
设AG与EF交于H,
在Rt△ABG中,AG2=BG2+AB2,
即AG2=22+62,
解得AG=2 ,
,
故HG=AF= ,
,
在Rt△AEH中,由勾股定理求出EH=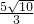 ,FH=
,FH= .
.
故EF=EH+FH=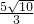 +
+ =2
=2 .
.
故答案为:2 .
.
点评:本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

分析:先根据题意画出图形,连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,再利用勾股定理求出AE的长,设DF=y,则CF=6-y,CG=4,再由等腰三角形的性质及勾股定理可求出EH、FH的值,进而可求出答案.
解答:
 解:连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,
解:连AG、AF、GF,可知EF是AG的垂直平分线,故GF=AF,设AE=GE=x,则BE=6-x,BG=2,
在Rt△BEG中,由勾股定理得EG2=BE2+BG2,
即x2=(6-x)2+22,
解得x=
 ,
,设DF=y,则CF=6-y,CG=4,在Rt△ADF中,
AF2=AD2+DF2,即AF2=36+y2,
在Rt△CGF中,GF2=CG2+CF2,
由勾股定理得,
36+y2=(6-y)2+16,
解得y=
 ,
,设AG与EF交于H,
在Rt△ABG中,AG2=BG2+AB2,
即AG2=22+62,
解得AG=2
 ,
,故HG=AF=
 ,
,在Rt△AEH中,由勾股定理求出EH=
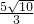 ,FH=
,FH= .
.故EF=EH+FH=
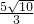 +
+ =2
=2 .
.故答案为:2
 .
.点评:本题考查的是图形翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 15、如图,在小方格的边长为1的方格纸中,将正方形ABCD先向右平移2格,再向下平移3格,得到正方形A′B′C′D′,则在正方形ABCD平移到正方形A′B′C′D′的过程中,所经过或覆盖的区域的面积为
15、如图,在小方格的边长为1的方格纸中,将正方形ABCD先向右平移2格,再向下平移3格,得到正方形A′B′C′D′,则在正方形ABCD平移到正方形A′B′C′D′的过程中,所经过或覆盖的区域的面积为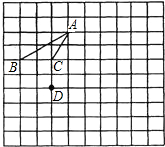 ,得到对应△A′B′C′.
,得到对应△A′B′C′.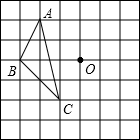 如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′)
如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′) 如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目
如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目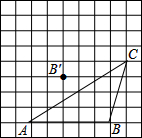 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.