题目内容
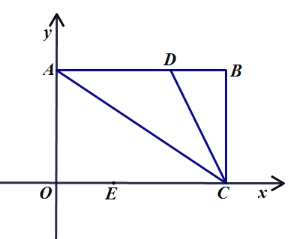
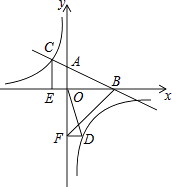
【题目】如图，在梯形
中，
，
，且
，分别以
、AB、
为边向梯形外作正方形，其面积分别为
、
、
，则、、之间数量的关系是（ ）
A.
B.
C.
D.
【答案】A
【解析】
过点A作AE∥BC交CD于点E，得到平行四边形ABCE和Rt△ADE，根据平行四边形的性质和勾股定理，不难证明三个正方形的边长对应等于所得直角三角形的边．
解：过点A作AE∥BC交CD于点E，
∵AB∥DC，
∴四边形AECB是平行四边形，
∴AB=CE，BC=AE，∠BCD=∠AED，
∵∠ADC+∠BCD=90°，DC=2AB，
∴AB=DE，∠ADC+∠AED=90°，
∴∠DAE=90°那么AD2+AE2=DE2，
∵S1=AD2，S2=AB2=DE2，S3=BC2=AE2，
∴S2=S1+S3．
故选：A．
练习册系列答案
相关题目
