题目内容
20.一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号和为4的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的小球标号和为4的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,两次摸出的小球标号和为4的有2种情况,
∴两次摸出的小球标号和为4的概率是:$\frac{2}{6}$=$\frac{1}{3}$.
故选B.
点评 此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
8.下列说法中正确的是( )
| A. | 篮球队员在罚球线上投篮一次,未投中是必然事件 | |
| B. | 想了解某种饮料中含色素的情况,宜采用普查 | |
| C. | 数据5,1,-2,2,3的中位数是-2 | |
| D. | 一组数据的波动越大,方差越大 |
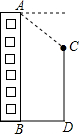 如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为11.6m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明在楼AB顶部的点A处测得楼前一棵树CD的顶端C的俯角为37°,已知楼AB高为18m,楼与树的水平距离BD为8.5m,则树CD的高约为11.6m(精确到0.1m).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)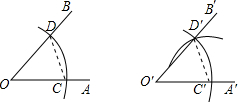 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( )
请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图,要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是( ) 如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y关于点P运动的时间x(单位:秒)的函数图象大致是( )