题目内容
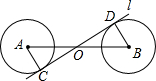 如图,两个等圆⊙A、⊙B分别与直线l相切于点C、D,连接AB,与直线l相交于点O,∠AOC=30°,连接AC.BC,若AB=4,则圆的半径为( )
如图,两个等圆⊙A、⊙B分别与直线l相切于点C、D,连接AB,与直线l相交于点O,∠AOC=30°,连接AC.BC,若AB=4,则圆的半径为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
分析:由两个等圆⊙A、⊙B分别与直线l相切于点C、D,根据切线的性质,即可得AC⊥CD,BD⊥CD,然后利用AAS即可判定△ACO≌△BDO,证得AO=BO=2,又由∠AOC=30°,即可求得圆的半径.
解答:解:∵两个等圆⊙A、⊙B分别与直线l相切于点C、D,
∴AC⊥CD,BD⊥CD,AC=BD,
∴∠ACO=∠BDO=90°,
在△ACO与△BDO中,
,
∴△ACO≌△BDO(AAS),
∴AO=BO=
AB=
×4=2,
∵∠AOC=30°,
∴AC=
AO=1.
故选B.
∴AC⊥CD,BD⊥CD,AC=BD,
∴∠ACO=∠BDO=90°,
在△ACO与△BDO中,
|
∴△ACO≌△BDO(AAS),
∴AO=BO=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC=30°,
∴AC=
| 1 |
| 2 |
故选B.
点评:此题考查了切线的性质,全等三角形的判定与性质以及直角三角形的性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 16、如图,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB=
16、如图,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,A、B是切点,则∠AOB=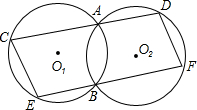 于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
 17、如图:两个等圆⊙A与⊙B外切,过A作⊙B的两条切线AC、AD,C、D是切点,则∠CAD=
17、如图:两个等圆⊙A与⊙B外切,过A作⊙B的两条切线AC、AD,C、D是切点,则∠CAD= (2004•包头)如图,两个等圆的圆心分别为O1、O2,⊙O1过点O2,两圆相交于P、Q两点,已知01O2=6cm,则阴影部分的周长是
(2004•包头)如图,两个等圆的圆心分别为O1、O2,⊙O1过点O2,两圆相交于P、Q两点,已知01O2=6cm,则阴影部分的周长是