题目内容
 如图,D、C、E三点共线,∠BAD=∠CAE,请结合现有图形,添加一个适当的条件:________,使得△ABC∽△ADE.
如图,D、C、E三点共线,∠BAD=∠CAE,请结合现有图形,添加一个适当的条件:________,使得△ABC∽△ADE.
此题答案不唯一,如∠B=∠D或∠ACB=∠E或 或AB•AE=AD•AC等
或AB•AE=AD•AC等
分析:由∠BAD=∠CAE,可得∠BAC=∠DAE,根据有两角对应相等的三角形相似,即可得当∠B=∠D或∠ACB=∠E时,△ABC∽△ADE;根据两组对应边的比相等且夹角对应相等的两个三角形相似,可得当 或AB•AE=AD•AC时,△ABC∽△ADE.
或AB•AE=AD•AC时,△ABC∽△ADE.
解答:∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∴当∠B=∠D或∠ACB=∠E或 或AB•AE=AD•AC时,△ABC∽△ADE.
或AB•AE=AD•AC时,△ABC∽△ADE.
故答案为:此题答案不唯一,如∠B=∠D或∠ACB=∠E或 或AB•AE=AD•AC等.
或AB•AE=AD•AC等.
点评:此题考查了相似三角形的判定.此题难度不大,属于开放性题目,注意掌握有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似定理的应用,注意数形结合思想的应用.
 或AB•AE=AD•AC等
或AB•AE=AD•AC等分析:由∠BAD=∠CAE,可得∠BAC=∠DAE,根据有两角对应相等的三角形相似,即可得当∠B=∠D或∠ACB=∠E时,△ABC∽△ADE;根据两组对应边的比相等且夹角对应相等的两个三角形相似,可得当
 或AB•AE=AD•AC时,△ABC∽△ADE.
或AB•AE=AD•AC时,△ABC∽△ADE.解答:∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∴当∠B=∠D或∠ACB=∠E或
 或AB•AE=AD•AC时,△ABC∽△ADE.
或AB•AE=AD•AC时,△ABC∽△ADE.故答案为:此题答案不唯一,如∠B=∠D或∠ACB=∠E或
 或AB•AE=AD•AC等.
或AB•AE=AD•AC等.点评:此题考查了相似三角形的判定.此题难度不大,属于开放性题目,注意掌握有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
 9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
9、如图,A、C、E三点在同一条直线上,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( ) 15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )
15、如图,A、Q、R三点在一条直线上,S为直线外一点,∠AQS=136°,∠QRS=64°,则∠QSR=( )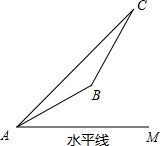 车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(
车站B的仰角为30°,AB间缆绳长500米(自然弯曲忽略不计).(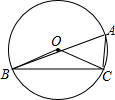 如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )
如图,A、B、C三点在⊙O上,∠BAC=60°,若⊙O的半径OC为12,则劣弧BC的长为( )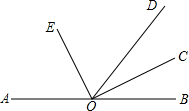 如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?
如图,A,O,B三点在同一直线上,OC,OE分别是∠BOD,∠AOD的平分线,OC与OE有什么位置关系?为什么?