题目内容
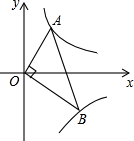 已知点A,B分别在反比例函数y=
已知点A,B分别在反比例函数y= (x>0),y=
(x>0),y= (x>0)的图象上且OA⊥OB,则tanB为
(x>0)的图象上且OA⊥OB,则tanB为
- A.

- B.

- C.

- D.

B
分析:首先设出点A和点B的坐标分别为:(x1, )、(x2,-
)、(x2,- ),设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,然后根据OA⊥OB,得到k1k2=
),设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,然后根据OA⊥OB,得到k1k2= •(-
•(-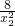 )=-1,然后利用正切的定义进行化简求值即可.
)=-1,然后利用正切的定义进行化简求值即可.
解答:设点A的坐标为(x1, ),点B的坐标为(x2,-
),点B的坐标为(x2,- ),
),
设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,
则k1= ,k2=-
,k2=-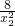 ,
,
∵OA⊥OB,
∴k1k2= •(-
•(-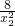 )=-1
)=-1
整理得:(x1x2)2=16,
∴tanB= =
=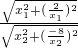 =
=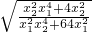 =
=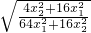 =
=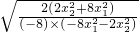 =
=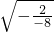 =
= .
.
故选B.
点评:本题考查的是反比例函数综合题,解题的关键是设出A、B两点的坐标,然后利用互相垂直的两条直线的比例系数互为负倒数求解.
分析:首先设出点A和点B的坐标分别为:(x1,
 )、(x2,-
)、(x2,- ),设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,然后根据OA⊥OB,得到k1k2=
),设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,然后根据OA⊥OB,得到k1k2= •(-
•(-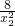 )=-1,然后利用正切的定义进行化简求值即可.
)=-1,然后利用正切的定义进行化简求值即可.解答:设点A的坐标为(x1,
 ),点B的坐标为(x2,-
),点B的坐标为(x2,- ),
),设线段OA所在的直线的解析式为:y=k1x,线段OB所在的直线的解析式为:y=k2x,
则k1=
 ,k2=-
,k2=-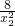 ,
,∵OA⊥OB,
∴k1k2=
 •(-
•(-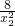 )=-1
)=-1整理得:(x1x2)2=16,
∴tanB=
 =
=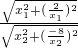 =
=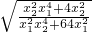 =
=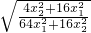 =
=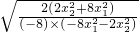 =
=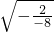 =
= .
.故选B.
点评:本题考查的是反比例函数综合题,解题的关键是设出A、B两点的坐标,然后利用互相垂直的两条直线的比例系数互为负倒数求解.

练习册系列答案
相关题目