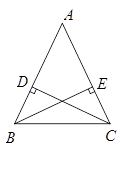
题目内容
证明:等腰三角形两腰中点的连线与底边上的高互相垂直且平分.分析:可根据三角形中位线定理,证得以等腰三角形顶角顶点、两腰及底边中点为顶点的四边形是菱形,然后根据菱形的对角线互相垂直平分来得出所求的结论.
解答:已知:如图△ABC中,AB=AC,D、E分别为AB、AC的中点,AF为BC上的高.
求证:AF、DE互相垂直平分.
证明:连DF,EF,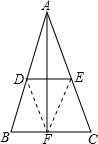
∵D、E、F分别为AB、AC、BC的中点,
∴DE、DF、EF分别△ABC的中位线,
∴EF=
AB,DF=
AC,
且AD=
AB,AE=
AC.
又AB=AC,
∴AD=DF=EF=AE.
∴四边形ADFE为菱形.
∴AF、DE互相垂直平分.
求证:AF、DE互相垂直平分.
证明:连DF,EF,

∵D、E、F分别为AB、AC、BC的中点,
∴DE、DF、EF分别△ABC的中位线,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
且AD=
| 1 |
| 2 |
| 1 |
| 2 |
又AB=AC,
∴AD=DF=EF=AE.
∴四边形ADFE为菱形.
∴AF、DE互相垂直平分.
点评:此题主要考查了三角形中位线定理、等腰三角形的性质、菱形的判定和性质.

练习册系列答案
相关题目
 证明命题“等腰三角形两腰上的高线相等”.
证明命题“等腰三角形两腰上的高线相等”.