题目内容
4.(|x+1|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+1|)=36,取x+y-z的最大值和最小值.分析 直接利用绝对值的性质得出:|x+l|+|x-2|≥3,|y-2|+|y+1|≥3,|z-3|+|z+l|≥4,进而利用已知得出答案.
解答 解:∵|x+l|+|x-2|≥3,
|y-2|+|y+1|≥3,
|z-3|+|z+l|≥4,
∴(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)≥36,
∵(|x+l|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+l|)=36,
∴|x+l|+|x-2|=3,|y-2|+|y+1|=3,|z-3|+|z+l|=4,
∴-1≤x≤2,-1≤y≤2,-1≤z≤3,
∴-5≤x+y-z≤5,
故最大值5,最小值-5.
点评 此题主要考查了绝对值,正确得出x,y,z的取值范围是解题关键.

练习册系列答案
相关题目
14.森林公园的门票价格规定如表:
某校初一(5)(6)两个班共104人去游森林公园,其中(5)班人数较少,不到50人,(6)班人数较多,(6)班人数多于50人且少于100人,经估算,如果两班都是以班为单位分别购票则一共应付1240元;
(1)求这两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 9元 |
(1)求这两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
9.设n为正整数,且n<$\sqrt{51}$<n+1,则n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
13.已知点M(1,-3),点M关于x轴的对称点的坐标是( )
| A. | (-1,3) | B. | (-1,-3) | C. | (3,1) | D. | (1,3) |
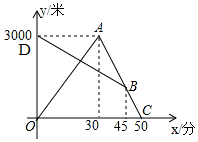 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题: