题目内容
已知:如图所示的一张矩形纸片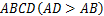 ,将纸片折叠一次,使点
,将纸片折叠一次,使点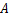 与
与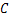 重合,再展开,折痕
重合,再展开,折痕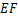 交
交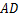 边于
边于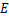 ,交
,交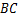 边于
边于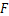 ,分别连接
,分别连接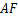 和
和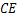 .
.
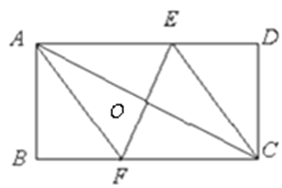
(1)求证:四边形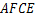 是菱形.
是菱形.
(2)若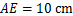 ,△
,△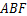 的面积为
的面积为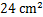 ,求△
,求△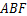 的周长.
的周长.
(3)在线段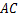 上是否存在一点
上是否存在一点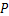 ,使得
,使得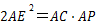 ?若存在,请说明点
?若存在,请说明点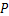 的位置,并予以证明;若不存在,请说明理由.
的位置,并予以证明;若不存在,请说明理由.
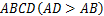 ,将纸片折叠一次,使点
,将纸片折叠一次,使点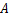 与
与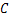 重合,再展开,折痕
重合,再展开,折痕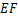 交
交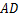 边于
边于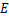 ,交
,交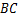 边于
边于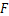 ,分别连接
,分别连接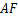 和
和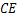 .
.
(1)求证:四边形
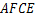 是菱形.
是菱形.(2)若
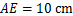 ,△
,△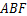 的面积为
的面积为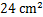 ,求△
,求△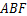 的周长.
的周长.(3)在线段
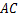 上是否存在一点
上是否存在一点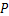 ,使得
,使得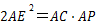 ?若存在,请说明点
?若存在,请说明点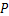 的位置,并予以证明;若不存在,请说明理由.
的位置,并予以证明;若不存在,请说明理由.(1)见解析 (2)24 (3)存在,理由见解析
(1)证明:由题意可知
∵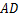 ∥
∥ ∴∠
∴∠ ∠
∠ ,∠
,∠ =∠
=∠ ∴△
∴△ ≌△
≌△
∵ ,又
,又 ∥
∥ ∴四边形
∴四边形 是平行四边形.
是平行四边形.
∵ ,∴ 平行四边形
,∴ 平行四边形 是菱形.
是菱形.
(2)解:∵ 四边形 是菱形,∴
是菱形,∴ .
.
设 ,∵△
,∵△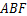 的面积为24,
的面积为24,

△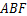 的周长为
的周长为 .
.
(3)解:存在,过点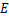 作
作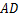 的垂线,交
的垂线,交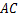 于点
于点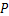 ,点
,点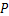 就是符合条件的点.
就是符合条件的点.
证明如下:
∵∠ ∠
∠ 90°,∠
90°,∠ ∠
∠
∴△ ∽△
∽△ ,∴
,∴ ,∴
,∴ .
.
∵ 四边形 是菱形,∴
是菱形,∴
∴ ∴
∴

∵
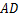 ∥
∥ ∴∠
∴∠ ∠
∠ ,∠
,∠ =∠
=∠ ∴△
∴△ ≌△
≌△
∵
 ,又
,又 ∥
∥ ∴四边形
∴四边形 是平行四边形.
是平行四边形. ∵
 ,∴ 平行四边形
,∴ 平行四边形 是菱形.
是菱形.(2)解:∵ 四边形
 是菱形,∴
是菱形,∴ .
.设
 ,∵△
,∵△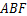 的面积为24,
的面积为24,

△
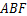 的周长为
的周长为 .
.(3)解:存在,过点
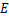 作
作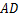 的垂线,交
的垂线,交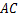 于点
于点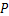 ,点
,点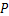 就是符合条件的点.
就是符合条件的点.证明如下:
∵∠
 ∠
∠ 90°,∠
90°,∠ ∠
∠
∴△
 ∽△
∽△ ,∴
,∴ ,∴
,∴ .
.∵ 四边形
 是菱形,∴
是菱形,∴
∴
 ∴
∴

练习册系列答案
相关题目

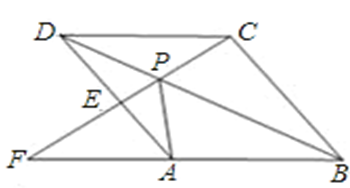
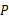 是菱形
是菱形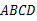 的对角线
的对角线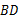 上一点,连接
上一点,连接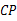 并延长,交
并延长,交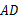 于
于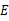 ,交
,交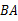 的延长线于点
的延长线于点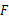 .
.
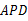 与哪个三角形全等?并说明理由.
与哪个三角形全等?并说明理由.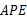 ∽△
∽△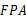 .
.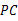 ,
,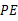 ,
,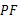 之间存在什么关系?并说明理由.
之间存在什么关系?并说明理由.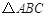 中,
中, ,
, 的垂直平分线
的垂直平分线 交
交 ,交
,交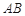 于点
于点 ,点
,点 在
在 .
.
 是平行四边形.
是平行四边形. 满足什么条件时,四边形
满足什么条件时,四边形 在向量
在向量 、
、 方向上的分向量分别是( )
方向上的分向量分别是( )
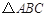 中,
中,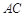 的垂直平分线分别交
的垂直平分线分别交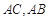 于点
于点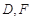 ,
, 交
交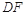 的延长线于点
的延长线于点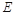 ,已知
,已知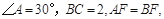 则四边形
则四边形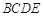 的面积是( )
的面积是( )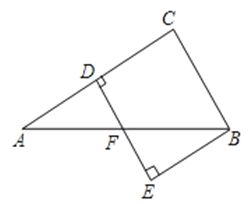

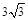

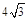
 cm,
cm, cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
cm,动点M从点D出发,按折线DCBAD方向以2 cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1 cm/s的速度运动.
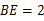 cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?
cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形? 中,对角线
中,对角线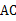 、
、 相交于点O,E为BC的中点,则下列式子中,一定成立的是( )
相交于点O,E为BC的中点,则下列式子中,一定成立的是( )



