题目内容
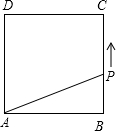 如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=x,四边形APCD的面积为y.
如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=x,四边形APCD的面积为y.(1)写出y与x之间的关系式,你能求出x的范围吗?
(2)当x为何值时,四边形APCD的面积为
| 3 | 2 |
(3)当点P由B向C运动时,四边形APCD的面积越来越大,还是越来越小?
分析:四边形APCD是一个梯形,根据梯形的面积公式求解;代入y=
,可求出x;根据函数式中k的特点可看出越来越大,还是越来越小.
| 3 |
| 2 |
解答:解:(1)设BP=x,四边形APCD的面积为y.
y=
×(2+2-x)×2
y=4-x(0≤x≤2)
(2)把y=
代入y=4-x得:4-x=
,
x=
.
(3)当点P由B向C运动时梯形的上底长越来越小,或者是根据一次函数k<0时,y随x的增大而减小可得四边形APCD的面积越来越小.
y=
| 1 |
| 2 |
y=4-x(0≤x≤2)
(2)把y=
| 3 |
| 2 |
| 3 |
| 2 |
x=
| 5 |
| 2 |
(3)当点P由B向C运动时梯形的上底长越来越小,或者是根据一次函数k<0时,y随x的增大而减小可得四边形APCD的面积越来越小.
点评:本题的关键是要看出四边形APCD是个什么样的四边形,然后根据函数的性质来判断越来越大还是越来越小.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
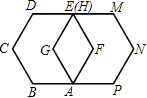 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,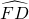 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.