题目内容
9. 如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是2.
如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是2.
分析 作PE⊥OA于E,利用余弦的定义求出PD,根据角平分线的性质解答即可.
解答 解: 作PE⊥OA于E,
作PE⊥OA于E,
∵∠OPD=60°,PO=4,
∴PD=OP×cos∠OPD=2,
∵OP平分∠AOB,PD⊥OB,PE⊥OA,
∴PE=PD=2,
故答案为:2.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.在下列图案中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.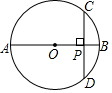 ⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
 ⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | $\sqrt{91}$cm |
18. 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD的度数是( )
如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD的度数是( )
 如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD的度数是( )
如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,D为第一象限内⊙O上的一点,若∠DAB=25°,则∠OCD的度数是( )| A. | 45° | B. | 60° | C. | 65° | D. | 70° |
 如图,△ABC≌△DEC,则结论①BC=EC,②∠DCA=∠ACE,③CD=AC,④∠DCA=∠ECB,其中结论正确的个数是( )
如图,△ABC≌△DEC,则结论①BC=EC,②∠DCA=∠ACE,③CD=AC,④∠DCA=∠ECB,其中结论正确的个数是( )