题目内容
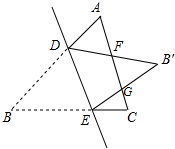 已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=75°,则∠EGC的度数为
已知等边△ABC中,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在点B′处,DB′、EB′分别交边AC于点F、G,若∠ADF=75°,则∠EGC的度数为考点:翻折变换(折叠问题)
专题:
分析:如图,由翻折变换的性质得到∠BDE=∠B′DE(设为α),∠BED=∠B′ED(设为β);求出2α=105°,
2β=135°,借助三角形外角的性质,即可解决问题.
2β=135°,借助三角形外角的性质,即可解决问题.
解答: 解:如图,由题意得:
解:如图,由题意得:
∠BDE=∠B′DE(设为α),∠BED=∠B′ED(设为β);
∵∠ADF=75°,
∴2α=180°-75°=105°;
∵△ABC为等边三角形,
∴∠B=∠C=60°,α+β=180°-60°=120°;
∴2β=240°-2α=135°;
∴∠EGC=2β-∠C=135°-60°=75°,
故答案为75°.
 解:如图,由题意得:
解:如图,由题意得:∠BDE=∠B′DE(设为α),∠BED=∠B′ED(设为β);
∵∠ADF=75°,
∴2α=180°-75°=105°;
∵△ABC为等边三角形,
∴∠B=∠C=60°,α+β=180°-60°=120°;
∴2β=240°-2α=135°;
∴∠EGC=2β-∠C=135°-60°=75°,
故答案为75°.
点评:该题主要考查了翻折变换的性质及其应用问题;灵活运用三角形的内角和定理、外角的性质是解题的关键.

练习册系列答案
相关题目
关于x的方程x2+(k2-1)x+2k+1=0的两根互为相反数,则k的值为( )
| A、-1 | B、1 | C、±1 | D、不能确定 |
若a+b+c=0,则
+
+
+
+
+
+
的值为( )
| |a| |
| a |
| |b| |
| b |
| |c| |
| c |
| |ab| |
| ab |
| |ac| |
| ac |
| |bc| |
| bc |
| |abc| |
| abc |
| A、-7 | B、-1 | C、1 | D、7 |
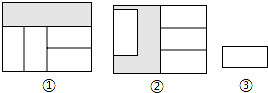 在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a的代数式表示)
在两个形状、大小完全相同的大长方形内,分别互不重叠地放入四个如图③的小长方形后得图①,图②,已知大长方形的长为a,两个大长方形未被覆盖部分分别用阴影表示,则图①阴影部分周长与图②阴影部分周长的差是( )(用a的代数式表示)| A、-a | ||
| B、a | ||
C、-
| ||
D、
|
如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
| A、矩形 | B、线段 |
| C、平行四边形 | D、一个点 |
 如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )
如图,△ABC中,点D在线段AB上,且∠BAD=∠C,则下列结论一定正确的是( )| A、AB2=AC•BD |
| B、AB•AD=BD•BC |
| C、AB2=BC•BD |
| D、AB•AD=BD•CD |