题目内容
 如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD,求证:∠1+∠2=90°.
如图所示,已知:AE平分∠BAC,CE平分∠ACD,且AB∥CD,求证:∠1+∠2=90°.考点:平行线的性质
专题:证明题
分析:根据两直线平行,同旁内角互补可得∠BAC+∠ACD=180°,根据角平分线的定义可得∠1=
∠BAC,∠2=
∠ACD,然后整理即可得证.
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠1=
∠BAC,∠2=
∠ACD,
∴∠1+∠2=
(∠BAC+∠ACD)=
×180°=90°.
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了平行线的性质,角平分线的定义,是基础题,熟记性质是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
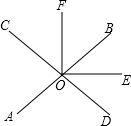 如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.
如图,直线AB与CD相交于点O,OE平分∠BOD,OF⊥OE于点O,若∠AOC=60°,求∠BOF的度数.