题目内容
阅读理解:对于任意正实数a,b,因为
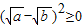 ,所以
,所以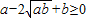 ,所以
,所以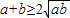 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.结论:在
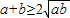 (a,b均为正实数)中,若ab为定值p,则
(a,b均为正实数)中,若ab为定值p,则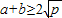 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值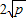 .
.(1)根据上述内容,回答下列问题:若m>0,只有当m=______时,
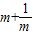 有最小值______;
有最小值______;(2)探索应用:如图,有一均匀的栏杆,一端固定在A点,在离A端2米的B处垂直挂着一个质量为8千克的重物.若已知每米栏杆的质量为0.5千克,现在栏杆的另一端C用一个竖直向上的拉力F拉住栏杆,使栏杆水平平衡.试问栏杆多少长时,所用拉力F最小?是多少?

【答案】分析:(1)根据题设所得的结论即可解答;
(2)根据杠杆原理先列出F的函数式,再利用几何不等式求解即可.
解答:解:(1)由题设的结论可得:当m=1, 有最小值为2.
有最小值为2.
(2)根据杠杆定理可得:Fx=2×8+0.5x× ,
,
F=
 =4,
=4,
当且仅当 ,x=8时,等号成立.
,x=8时,等号成立.
即当x=8m时,F最小=4千克=39.4牛.
故答案为:1,2.
点评:本题考查几何不等式的知识,难度不大,关键是读懂题意,灵活应用题中所给的结论解题.
(2)根据杠杆原理先列出F的函数式,再利用几何不等式求解即可.
解答:解:(1)由题设的结论可得:当m=1,
 有最小值为2.
有最小值为2.(2)根据杠杆定理可得:Fx=2×8+0.5x×
 ,
,F=

 =4,
=4,当且仅当
 ,x=8时,等号成立.
,x=8时,等号成立.即当x=8m时,F最小=4千克=39.4牛.
故答案为:1,2.
点评:本题考查几何不等式的知识,难度不大,关键是读懂题意,灵活应用题中所给的结论解题.

练习册系列答案
相关题目
 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少? 阅读理解:对于任意正实数a,b,
阅读理解:对于任意正实数a,b,
 阅读理解:
阅读理解: