题目内容
已知实数a,b满足a2+ab+b2=1,则t=a2-ab+b2的取值范围为________.
 ≤t≤3
≤t≤3分析:由两个等式可求出a+b、ab的表达式,这样既可以从配方法入手,又能从构造方程的角度去探索,有较大的思维空间.
解答:由已知得,ab=
 ,a+b=±
,a+b=± (t≤3),
(t≤3),∴a,b是关于方程x2±
 x+
x+ =0的两个实根,
=0的两个实根,由△=
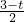 -2(1-t)≥0,
-2(1-t)≥0,解得t≥
 ,
,故t的取值范围是
 ≤t≤3.
≤t≤3.故答案为:
 ≤t≤3.
≤t≤3.点评:本题考查了一元二次方程根与系数的关系,方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .
. 
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知实数a、b满足a<b,则下列式子中正确的是( )
A、
| ||||
| B、b-a>0 | ||||
| C、a2<b2 | ||||
| D、a4<b4 |