Question

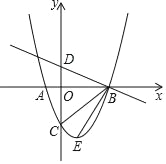
【题目】如图，已知抛物线y＝ax2+c过点（﹣2，2），（4，5），过定点F（0，2）的直线l：y＝kx+2与抛物线交于A、B两点，点B在点A的右侧，过点B作x轴的垂线，垂足为C．

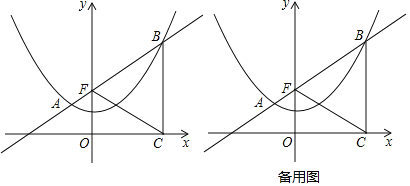
（1）求抛物线的解析式；

（2）当点B在抛物线上运动时，判断线段BF与BC的数量关系　 　（＞、＜、＝），并证明你的判断；

（3）P为y轴上一点，以B、C、F、P为顶点的四边形是菱形，设点P（0，m），求自然数m的值；

Answer 1

【答案】（1）y＝x2+1；（2）＝,理由见解析；（3）m的值为6．

【解析】

（1）把点（-2，2），（4，5）代入y=ax2+c，即可求解；

（2）设B （x，x2+1），而F（0，2），

则BF2=x2+（x2+1-2）2=x2+（x2-1）2=（x2+1）2，BC=x2+1，故BF=BC；

（3）当m=0时，则四边形BCPF为正方形，此时P点在原点；当点P在F点上方，以B、C、F、P为顶点的四边形是菱形，则CB=CF=PF，则△BCF为等边三角形，CF=2OF=4，PF=CF=4，即可求解．

解：（1）把点（﹣2，2），（4，5）代入y＝ax2+c得：，解得：，

所以抛物线解析式为y＝x2+1；

（2）设B（x，x2+1），而F（0，2），

∴BF2＝x2+（x2+1﹣2）2＝x2+（x2﹣1）2＝（x2+1）2，

∴BF＝x2+1，

∵BC⊥x轴，

∴BC＝x2+1，

∴BF＝BC，

答案为：＝

（3）如图，m为自然数，

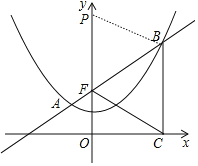
①当点P在F点上方，

∵以B、C、F、P为顶点的四边形是菱形，

∴CB＝CF＝PF，

而CB＝FB，

∴BC＝CF＝BF，

∴△BCF为等边三角形，

∴∠BCF＝60°，

∴∠OCF＝30°，

在Rt△OCF中，CF＝2OF＝4，

∴PF＝CF＝4，

∴P（0，6）；

②当点P在点F下方时，

PF＝BC＝4，而OF＝2，

则OP＝2，故m＝﹣2（舍去）；

③当m＝0时，

FP＝2，但是BC＝4，故不符合要求；

综上，自然数m的值为6．