Question

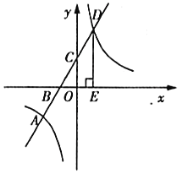
【题目】如图所示，在平面直角坐标系中，一次函数与反比例函数交于、两点，与轴交于点，作轴，垂足为，已知，．

（1）求一次函数与反比例函数的解析式；

（2）连接、，在轴取点，使与面积相等，求点坐标．

Answer 1

【答案】（1）；；（2）（2,0）或（-4,0）.

【解析】

（1）根据题意，结合直角三角形求解，得出点B、C的坐标代入一次函数，可得直线解析式，进而求出点D，可求出反比例函数的解析式即可；

（2）联立方程组求出点A，进而求出的面积，根据与面积相等列出关于底边长的一次方程求解即可．

（1）在Rt△COB中，OB=1，，

∴CO=，

将点B（-1，0），点C（0，）代入，得

，

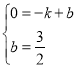解得，

∴，

∵CO⊥x轴，DE⊥x轴，OB=OE，

∴CO为△BED的中位线，

∴DE=2CO=3，

∴点D的坐标为（1，3），

∴将（1，3）代入，得m=3，

∴，

故答案为：；；

（2）连接DO、AO，

将与联立方程组，得

，

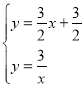解得或，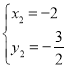

∴点A坐标为（-2，），D（1,3），

∴，

设△CBF的底边长为a，

可得：，

解得：a=3，

∴点F的坐标为（-1+3，0），（-1-3，0），

即点F的坐标为（2，0）或（-4，0），

故答案为：（2，0）或（-4，0）．