题目内容
三角形的两边长分别为4和5,那么第三边a的取值范围是 .
考点:三角形三边关系
专题:
分析:根据三角形的任意两边之和大于第三边,两边之差小于第三边求出第三边a的取值范围.
解答:解:∵三角形的两边长分别为4和5,第三边的长为a,
∴根据三角形的三边关系,得:5-4<a<5+4,即:1<a<9.
故答案为:1<a<9.
∴根据三角形的三边关系,得:5-4<a<5+4,即:1<a<9.
故答案为:1<a<9.
点评:此题考查了三角形的三边关系.此题比较简单,注意掌握已知三角形两边,则第三边的长度应是大于两边的差而小于两边的和.

练习册系列答案
相关题目
对于一元二次方程x2-bx+c=0,下面的结论错误的是( )
| A、若c=0,则方程必有一根为0 |
| B、若c<0,则方程必有一正数根和一负数根 |
| C、若c>0,b<0,则方程必有两个正数根 |
| D、若b>c+1,则方程一个根大于-1、一个根小于-1 |
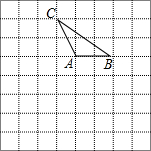 如图,在正方形组成的网格中,△ABC的三个顶点在格点上,现以△ABC的一边再作一个三角形,使所得的三角形与△ABC全等,且其顶点也在格点上,则这样的三角形有
如图,在正方形组成的网格中,△ABC的三个顶点在格点上,现以△ABC的一边再作一个三角形,使所得的三角形与△ABC全等,且其顶点也在格点上,则这样的三角形有 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转得△A′B′C,使点B′落在线段AB上,如果∠B=65°,则∠ACA′=
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转得△A′B′C,使点B′落在线段AB上,如果∠B=65°,则∠ACA′=