题目内容
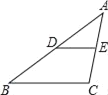
【题目】如图,在三角形![]() 中,
中,![]() .将三角形
.将三角形![]() 绕着点
绕着点![]() 旋转,使得点
旋转,使得点![]() 落在直线
落在直线![]() 上的点
上的点![]() ,点
,点![]() 落在点
落在点![]() .
.
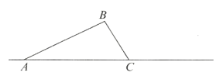
(1)画出旋转后的三角形![]() .
.
(2)求线段![]() 在旋转的过程中所扫过的面积(保留
在旋转的过程中所扫过的面积(保留![]() ).
).
(3)如果在三角形![]() 中,
中,![]() (其中
(其中![]() ).其他条件不变,请你用含有
).其他条件不变,请你用含有![]() 的代数式,直接写出线段
的代数式,直接写出线段![]() 旋转的过程中所扫过的面积(保留
旋转的过程中所扫过的面积(保留![]() ).
).
【答案】(1)见解析;(2)![]() 或
或![]() ;(3)
;(3)![]() 或者
或者![]()
【解析】
(1)分种顺时针和逆时针作图即可;
(2)根据逆时针转60度,顺时针转120度,分别计算面积;
(3)利用(1)的旋转图形与(2)的面积计算进行求解.
(1)分两种情况:逆时针旋转60°,如下图所示,

顺时针旋转120°,所下图所示,

(2)逆时针转60度:
![]()
![]()
![]()
![]()
顺时针转120度:
![]()
![]()
![]()
![]()
(3)由(1)可知,当![]() 时,需要逆时针旋转
时,需要逆时针旋转![]() 或顺时针旋转
或顺时针旋转![]() ,
,
同(2)的面积计算可得:
逆时针转![]() 度:
度:
![]()
顺时针转![]() 度:
度:
![]()
故答案为:![]() 或者
或者![]()

练习册系列答案
相关题目