题目内容
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.

(1)证明:如图,

连接OD.
∵AB=AC,
∴∠B=∠C,
∵OD=OC,
∴∠ODC=∠C,
∴∠ODC=∠B,
∴OD∥AB,
∵DF⊥AB,
∴OD⊥DF,
∵点D在⊙O上,
∴直线DF与⊙O相切;
(2)解:∵四边形ACDE是⊙O的内接四边形,
∴∠AED+∠ACD=180°,
∵∠AED+∠BED=180°,
∴∠BED=∠ACD,
∵∠B=∠B,
∴△BED∽△BCA,
∴ =
= ,
,
∵OD∥AB,AO=CO,
∴BD=CD= BC=3,
BC=3,
又∵AE=7,
∴ =
= ,
,
∴BE=2,
∴AC=AB=AE+BE=7+2=9.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下面四个立体图形中,三视图完全相同的是( )
|
| A. |
| B. |
| C. |
| D. |
|
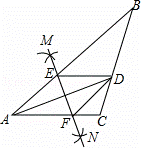
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于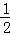 AD的长为半径在AD两侧作弧,交于两点M、N;
AD的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( )
|
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
如图所示的几何体的主视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
二次函数y=x2+4x﹣5的图象的对称轴为( )
|
| A. | x=4 | B. | x=﹣4 | C. | x=2 | D. | x=﹣2 |
如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是( )

|
| A. | 2015π | B. | 3019.5π | C. | 3018π | D. | 3024π |




 )0+|﹣2015|﹣4cos60°.
)0+|﹣2015|﹣4cos60°.