题目内容
12.抛物线y=-x2+4x+m-2的顶点恰好是另一条抛物线y=2x2+nx+11的顶点,求m,n的值.分析 分别求得两抛物线的顶点坐标可得到关于m、n的方程,可求得m、n的值.
解答 解:
∵y=-x2+4x+m-2=-(x-2)2+m+2,
∴顶点坐标为(2,m+2),
∴对称轴为x=2,
∴抛物线y=2x2+nx+11的对称轴为x=2,
∴-$\frac{n}{2×2}$=2,解得n=-8,
∴抛物线y=2x2+nx+11解析式为y=2x2-8x+11=2(x-2)2+3,
∴顶点坐标为(2,3),
∴m+2=3,解得m=1,
综上可知m为1,n为-8.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
3. 一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
 一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )
一种足球是由32块黑白相间的牛皮缝制而成的(如图,黑皮可看做正五边形,白皮可看做正六边形).设黑皮有x块,则白皮有(32-x)块.下面所列的方程正确的是( )| A. | 3(32-x)=x | B. | 3(32-x)=5x | C. | 5(32-x)=3x | D. | 6(32-x)=x |
20.⊙O的半径r=5cm,点P在直线l上,若OP=6cm,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
7.分式方程$\frac{1}{x+1}$+$\frac{1}{{x}^{2}+x}$=0去分母应乘的最简公分母是( )
| A. | x+1 | B. | x2 | C. | x(x+1) | D. | x(x+1)2 |
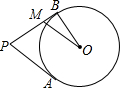 如图,PA、PB分别与⊙O相切于A、B,点M在PB上,且OM∥AP,若⊙O的半径r=3,PA=9,求OM的长.
如图,PA、PB分别与⊙O相切于A、B,点M在PB上,且OM∥AP,若⊙O的半径r=3,PA=9,求OM的长. 如图,过反比例函数y=$\frac{6}{x}$(x>0)图象上一点A作x轴的平行线,交双曲线y=-$\frac{3}{x}$(x<0)于点B,过B作BC∥OA交双曲线y=-$\frac{3}{x}$(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,求OE的长.
如图,过反比例函数y=$\frac{6}{x}$(x>0)图象上一点A作x轴的平行线,交双曲线y=-$\frac{3}{x}$(x<0)于点B,过B作BC∥OA交双曲线y=-$\frac{3}{x}$(x<0)于点D,交x轴于点C,连接AD交y轴于点E.若OC=3,求OE的长.