题目内容
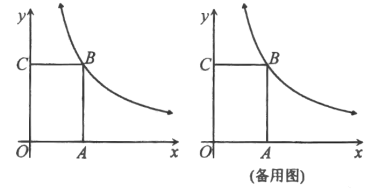
【题目】如图,矩形![]() 的顶点
的顶点![]() 分别在
分别在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.
【答案】(1)点P的坐标为(6,2);(2)![]() ;(3)Q
;(3)Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
【解析】
(1)首先根据点B坐标,确定反比例函数的解析式,设点P的纵坐标为m(m>0),根据![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
(2)过点(0,2),作直线l⊥y轴,由(1)知,点P的纵坐标为2,推出点P在直线l上作点O关于直线l的对称点O',则OO'=4,连接AO'交直线l于点P,此时PO+PA的值最小;
(3)分两种情形分别求解即可解决问题;
(1)∵四边形OABC是矩形,OA=4,OC=3,
∴点B的坐标为(4,3),
∵点B在反比例函数![]() 的第一象限内的图象上
的第一象限内的图象上
∴k=12,
∴y=![]() ,
,
设点P的纵坐标为m(m>0),
∵![]() .
.
∴![]() OAm=OAOC
OAm=OAOC![]() ,
,
∴m=2,
当点,P在这个反比例函数图象上时,则2=![]() ,
,
∴x=6
∴点P的坐标为(6,2).
(2)过点(0,2),作直线l⊥y轴.
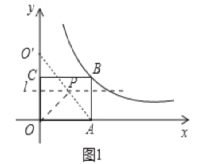
由(1)知,点P的纵坐标为2,
∴点P在直线l上
作点O关于直线l的对称点O',则OO'=4,
连接AO'交直线l于点P,此时PO+PA的值最小,
则PO+PA的最小值=PO'+PA=O'A=![]() .
.
(3)
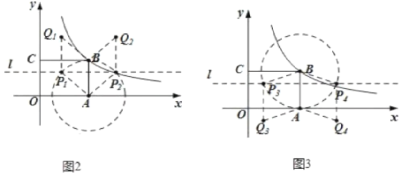
①如图2中,当四边形ABQP是菱形时,易知AB=P=PQ=BQ=3,P![]() (4
(4![]() ,2),P
,2),P![]() (4
(4![]() ,2),
,2),
∴Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5).
,5).
②如图3中,当四边形ABPQ是菱形时,P![]() (42
(42![]() ,2),P
,2),P![]() (4+2
(4+2![]() ,2),
,2),
∴Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).
综上所述,点Q的坐标为Q![]() (4
(4![]() ,5),Q
,5),Q![]() (4+
(4+![]() ,5),Q
,5),Q![]() (42
(42![]() ,1),Q
,1),Q![]() (4+2
(4+2![]() ,1).
,1).

 一本好题口算题卡系列答案
一本好题口算题卡系列答案