题目内容
 12、如图所示,等腰△ABC中,底边BC上有任意一点D,则D点到两腰上的距离与一腰上的高有什么关系?
12、如图所示,等腰△ABC中,底边BC上有任意一点D,则D点到两腰上的距离与一腰上的高有什么关系?(1)在甲图中,当点D在底边BC上时,写出你的猜想并证明;
(2)在乙图中,当点D在BC的延长线上时,写出你的猜想并证明.
分析:(1)猜想是DE+DF=CG.在CG上截取CH=DE,连接DH,易证四边形GEDH是矩形,从而可知∠GHD=90°,DH∥AB,那么就有∠DHC=∠CFD=90°,∠HDC=∠B,又AB=AC,利用等边对等角,可得∠B=∠FCD,于是∠HDC=∠FCD,再结合CD=DC,利用AAS可证△DHC≌△CFD,那么CH=DF,从而易证DE+DF=CG.
(2)猜想:DE-DF=CG.过C作CM⊥ED,垂足为M,易证四边形CGEM是矩形,所以EM=DC,ED∥CG,于是∠1=∠3.由于AB=AC,利用等边对等角,可得∠B=∠ACB,而∠ACB=∠DCF,那么∠ACB=∠DCF,利用等角的余角相等,可得∠3=∠2.从而有∠1=∠2,显然利用AAS可证△DCM≌△DCF,那么DM=DF,易证
DE-DF=CG.
(2)猜想:DE-DF=CG.过C作CM⊥ED,垂足为M,易证四边形CGEM是矩形,所以EM=DC,ED∥CG,于是∠1=∠3.由于AB=AC,利用等边对等角,可得∠B=∠ACB,而∠ACB=∠DCF,那么∠ACB=∠DCF,利用等角的余角相等,可得∠3=∠2.从而有∠1=∠2,显然利用AAS可证△DCM≌△DCF,那么DM=DF,易证
DE-DF=CG.
解答: (1)猜想:DE+DF=CG.
(1)猜想:DE+DF=CG.
证明:如答图所示,在CG上
截取GH=ED,并连接HD,
∵CG⊥AB,DE⊥AB,
∴DE∥CG.
又GH=ED,
∴DHGE是矩形,
∴∠DHC=90°,
在△DHC和△CFD中,
∠DHC=∠CFD=90°,
∵DG∥AB,AB=AC,
∴∠HDC=∠B=∠FCD,DC=CD,
∴△DHC≌△CFD,
∴HC=FD,
∴DE+DF=GH+HC=CG,
即DE+DF=CG.
(2)猜想:DE-DF=CG.
证明:如答图所示,过C
作CM⊥ED,垂足为M,
∵DF⊥AC,
∴∠CMD=∠CFD=90°,
AB=AC,
∴∠B=∠ACB,
∵∠ACB=∠FCD,
∴∠B=∠FCD,
∵CG⊥AB,DE⊥AB,
∴∠3=90°-∠B,CG∥DE,
∴∠1=∠3,
又∵DF⊥CF,
∴∠2=90°-∠FCD.
∴∠2=90°-∠B,
∴∠1=∠2,
在△CMD和△CFD中,
∴△CMD≌△CFD,
∴DM=DF,
∵四边形GCME为长方形,
∴CG=EM,
∵EM+MD=DE,
∴CG+DF=DE,
即DE-DF=CG.
 (1)猜想:DE+DF=CG.
(1)猜想:DE+DF=CG.证明:如答图所示,在CG上
截取GH=ED,并连接HD,
∵CG⊥AB,DE⊥AB,
∴DE∥CG.
又GH=ED,
∴DHGE是矩形,
∴∠DHC=90°,
在△DHC和△CFD中,
∠DHC=∠CFD=90°,
∵DG∥AB,AB=AC,

∴∠HDC=∠B=∠FCD,DC=CD,
∴△DHC≌△CFD,
∴HC=FD,
∴DE+DF=GH+HC=CG,
即DE+DF=CG.
(2)猜想:DE-DF=CG.
证明:如答图所示,过C
作CM⊥ED,垂足为M,
∵DF⊥AC,
∴∠CMD=∠CFD=90°,
AB=AC,
∴∠B=∠ACB,
∵∠ACB=∠FCD,
∴∠B=∠FCD,
∵CG⊥AB,DE⊥AB,
∴∠3=90°-∠B,CG∥DE,
∴∠1=∠3,
又∵DF⊥CF,
∴∠2=90°-∠FCD.
∴∠2=90°-∠B,
∴∠1=∠2,
在△CMD和△CFD中,
∴△CMD≌△CFD,
∴DM=DF,
∵四边形GCME为长方形,
∴CG=EM,
∵EM+MD=DE,
∴CG+DF=DE,
即DE-DF=CG.
点评:本题考查了全等三角形的判定与性质及等腰三角形的性质;辅助线的作出是正确解答本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 30、如图所示,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,ED∥AB,则∠BCD等于( )
30、如图所示,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,ED∥AB,则∠BCD等于( )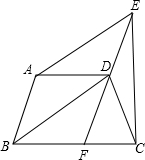 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.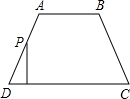 有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位.
有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位. 两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割的次数最多两次(切割的损失可以忽略不计).
两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割的次数最多两次(切割的损失可以忽略不计).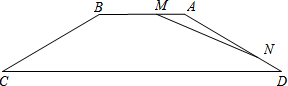 (2013•昌平区二模)如图所示,等腰梯形ABCD中,AB∥CD,AB=15,AD=20,∠C=30°.点M、N同时以相同的速度分别从点A、点D开始在AB、DA上向点B、点A运动.
(2013•昌平区二模)如图所示,等腰梯形ABCD中,AB∥CD,AB=15,AD=20,∠C=30°.点M、N同时以相同的速度分别从点A、点D开始在AB、DA上向点B、点A运动.