Question

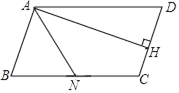
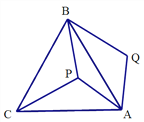
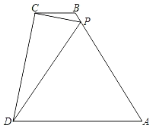
【题目】 如图，梯形ABCD中，BC∥AD，AB＝AD，P为边AB上一点，连PC，PD，CD垂直于CP且∠CPD＝∠A，BC＝4BP，则＝_____．

Answer 1

【答案】

【解析】

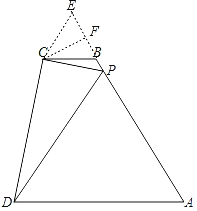
过点C作CF⊥AB交AB的延长线于点F，在AF的延长线上截取EF=BF，连接CE，设∠A＝∠CPD＝α，先证△ECP∽△APD，可得，在Rt△CDP中，＝cosα，设BP＝a，AD＝b，EF＝x，进而可得，由此计算即可得到答案．

解：过点C作CF⊥AB交AB的延长线于点F，在AF的延长线上截取EF=BF，连接CE，设∠A＝∠CPD＝α，

则CE＝BC，

∴∠CEB＝∠CBE，

∵BC∥AD，

∴∠A＝∠CBE，

∴∠A＝∠CEB＝∠CPD＝α，

∴∠CPE+∠DPA＝180°﹣α，

又∵∠PDA+∠DPA＝180°﹣α，

∴∠CPE＝∠PDA，

∴△ECP∽△APD，

∴，

在Rt△CDP中，＝cosα，

∴＝cosα＝，

设BP＝a，AD＝b，EF＝x，

∵BC＝4BP，AB＝AD，

∴CE＝BC＝4a，PA＝b﹣a，

∴，

解得：3b＝31a，

∴cosα＝．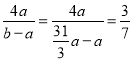

故答案为：．