Question

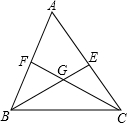如图，△ABC的∠B和∠C的平分线BE，CF相交于点G．
（1）若∠A=50°，求∠BGC；
（2）试探求∠BGC，∠A之间的数量关系，并证明你的结论．

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：

分析：（1）根据三角形的内角和是180°，可知∠BGC=180°-∠GBC-∠GCB，由BE，CF分别平分∠ABC，∠ACB，可知∠GBC=

1

2

∠ABC，∠GCB=

1

2

∠ACB，即∠BGC=180°-

1

2

（∠ABC+∠ACB），再由三角形的内角和是180°，得出∠ABC+∠ACB=180°-∠A，从而求出∠BGC的度数；
（2）∠BGC=90°+

1

2

∠A，由（1）可知：∠BGC=180°-

1

2

（∠ABC+∠ACB）=180°-

1

2

（180°-∠A）=90°+

1

2

∠A．

解答： 解：（1）∵BE，CF分别平分∠ABC，∠ACB，
∴∠GBC=

1

2

∠ABC，∠GCB=

1

2

∠ACB，
∵∠BGC=180°-∠GBC-∠GCB，
∴∠BGC=180°-

1

2

（∠ABC+∠ACB）
=180°-

1

2

（180°-∠A）
∵∠A=50°，
∴∠BGC=180°-

1

2

（180°-50°）=115°；
（2）∠BGC=90°+

1

2

∠A，
理由：
由（1）可知：∠BGC=180°-

1

2

（∠ABC+∠ACB）=180°-

1

2

（180°-∠A）=90°+

1

2

∠A

点评：主要考查了三角形的内角和是180度，及角平分线的定义．求角的度数常常要用到“三角形的内角和是180°这一隐含的条件