题目内容
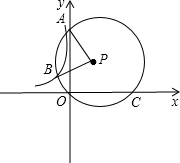 如图,⊙P过点O,A(0,4
如图,⊙P过点O,A(0,4| 2 |
| 2 |
| k |
| x |
分析:结合已知,可根据点O、A、C的坐标得出圆心P的坐标,和PA的长,然后过点P作PM⊥x轴于M,PN⊥y轴于N,过点B作BG⊥PM于点G,证明△ANP≌△PGB,从而求出点B的坐标,继而求出开的值.
解答: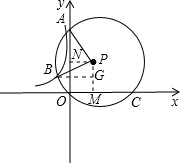 解:由已知得:
解:由已知得:
O(0,0),A(0,4
),C(2
,0),
∴得P(
,2
),
PA=PB=
.
过点P作PM⊥x轴于M,PN⊥y轴于N,过点B作BG⊥PM于点G,
由已知可得△ANP≌△PGB,
∴BG=AN=OA-0N=4
-2
=2
,
BG-PN=2
-
=
,
∴点B的横坐标为:-
.
∴GM=PM-PG=PM-PN=2
-
=
.
∴点B的坐标为:(-
,
),
∴
=
,
∴k=-2,
故答案为:2.
 解:由已知得:
解:由已知得:O(0,0),A(0,4
| 2 |
| 2 |
∴得P(
| 2 |
| 2 |
PA=PB=
| 10 |
过点P作PM⊥x轴于M,PN⊥y轴于N,过点B作BG⊥PM于点G,
由已知可得△ANP≌△PGB,
∴BG=AN=OA-0N=4
| 2 |
| 2 |
| 2 |
BG-PN=2
| 2 |
| 2 |
| 2 |
∴点B的横坐标为:-
| 2 |
∴GM=PM-PG=PM-PN=2
| 2 |
| 2 |
| 2 |
∴点B的坐标为:(-
| 2 |
| 2 |
∴
| 2 |
| k | ||
-
|
∴k=-2,
故答案为:2.
点评:本题主要考查了反比例函数的综合应用和圆的方程的应用,关键是运用正三角形全等得出答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )A、
| ||
B、2
| ||
C、3
| ||
D、
|
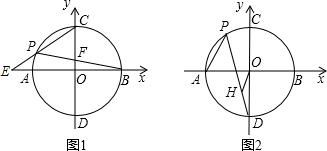
 如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
如图,⊙O过点B、C,圆心O在等腰Rt△ABC的内部,∠BAC=90°,OA=2,BC=8.则⊙O的半径为( )
 已知:如图A,△ABC各角的平分线AD,BE,CF交于点O.
已知:如图A,△ABC各角的平分线AD,BE,CF交于点O.