Question

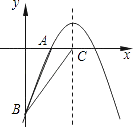
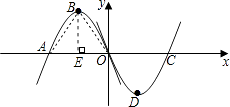
【题目】如图所示，抛物线y=ax2+bx（a＜0）的图象与x轴交于A、O两点，顶点为B，将该抛物线的图象绕原点O旋转180°后，与x轴交于点C，顶点为D，若此时四边形ABCD恰好为矩形，则b的值为 ．

Answer 1

【答案】﹣2
【解析】解：如图，连接AB、OB．过点B作BE⊥x轴于点E． 要使平行四边形ABCD是矩形，必须满足AC=BD，
∴OA=OB．
∵点B是抛物线的顶点，
∴AB=OB，
∴△ABO是等边三角形，
∠BAE=60°，AE= OA．
∵y=ax2+bx=ax（x+ ）=0，y=ax2+bx=a（x+ ）2﹣
∴A（﹣ ，0），B（﹣ ，﹣ ），
∴tan60°= = = ．
解得 b=﹣2 ．
故答案是：﹣2 ．

【考点精析】认真审题，首先需要了解二次函数图象的平移(平移步骤：（1）配方 y=a(x-h)2+k，确定顶点（h,k）（2）对x轴左加右减；对y轴上加下减)．