题目内容
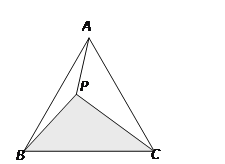
【题目】如图,在菱形ABCD中,边长为2![]() ,∠BAD=120°,点P从点B开始,沿着B→D方向,速度为每秒1个单位,运动到点D停止,设运动的时间为t(秒),将线段AP绕点A逆时针旋转60°,得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E,
,∠BAD=120°,点P从点B开始,沿着B→D方向,速度为每秒1个单位,运动到点D停止,设运动的时间为t(秒),将线段AP绕点A逆时针旋转60°,得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E,
(1)当t=0时,求AE的值.
(2)P点在运动过程中,线段PE与菱形的边框交于点F.(精确到0.1)
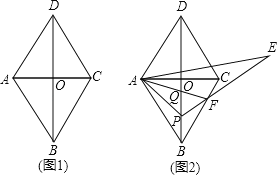
问题1:如图2,当∠BAP=11°,AF=2PF,则OQ= .
问题2:当t为何值时,△APF是含有30°角的直角三角形,写出所有符合条件的t的值 .
(![]() ≈1.73,sin11°≈0.19,cos11°≈0.98,sin19°≈0.33,tan19°≈0.34,sin41°≈0.65,tan41°≈0.87)
≈1.73,sin11°≈0.19,cos11°≈0.98,sin19°≈0.33,tan19°≈0.34,sin41°≈0.65,tan41°≈0.87)
(3)当点P在运动过程中,求出△ACE的面积y关于时间t的函数表达式.(请说明理由)
【答案】(1)AE=4![]() ;(2)问题1:OQ≈0.6,问题2:t=1s或4s时,∠PAF=30°;(3)S△ACE=
;(2)问题1:OQ≈0.6,问题2:t=1s或4s时,∠PAF=30°;(3)S△ACE=![]() t(0<t≤6)..
t(0<t≤6)..
【解析】
(1)利用直角三角形30度角的性质解决问题即可.
(2)①根据OQ=OAtan19°,求出OA即可解决问题.
②分两种情形:如图2-2中,当∠PAF=30°时,延长FP到H,使得PH=PF,连接AH,BH.如图2-1中,当∠PAF=30°,分别求解即可.
(3)如图3中,作BM⊥AB交AC的延长线于M,作EH⊥AM于H,连接EM.证明△EAM∽△PAB,推出![]() =2,求出EM即可解决问题.
=2,求出EM即可解决问题.
(1)t=0时,点P与点B重合,
∵∠PAE=60°,∠APE=60°,
∴∠E=30°,
∴AE=2PA=2AB=4![]() .
.
(2)①如图2中,
∵四边形ABCD是菱形,∠DAB=120°,
∴∠DAC=∠CAB=60°,AD=CD=AB=BC=2![]() ,
,
∴△ADC,△ABC都是等边三角形,
∴AC=AB=2![]() ,OA=OC=
,OA=OC=![]() ,
,
∵∠APF=90°,
∴sin∠PAF=![]() =
=![]() ,
,
∴∠PAF=30°,
∴∠OAQ=60°﹣11°﹣30°=19°,
∴OQ=OAtan19°≈0.6.
故答案为0.6.
②如图2﹣2中,当∠PAF=30°时,延长FP到H,使得PH=PF,连接AH,BH.
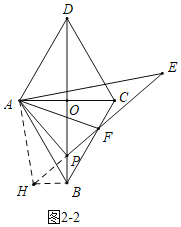
∵PA⊥FH,FP=FH,
∴AF=AH,
∵∠PAF=30°,
∴∠AFH=60°,
∴△AFH是等边三角形,
∴∠PAH=∠PAF=30°,
∴PA=![]() PH,
PH,
∵∠AHF=∠ABC
∴A,H,B,F四点共圆,
∴∠ABH=∠AFH=60°,
∴∠ABH=∠BAC=60°,
∴BH∥AC,
∵BD⊥AC,
∴BD⊥BH,
由△HBP∽△POA,可知:![]() =
=![]() ,
,
∴OA=![]() t,
t,
∴![]() =
=![]() t,
t,
∴t=1.
如图2﹣1中,当∠PAF=30°,易知∠BAP=90°,
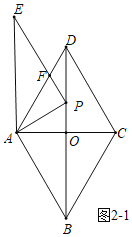
∴PB=![]() =
=![]() =4,
=4,
综上所述,t=1s或4s时,∠PAF=30°.
故答案为1s或4s.
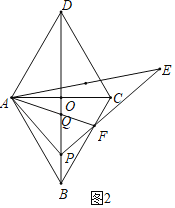
(3)如图3中,作BM⊥AB交AC的延长线于M,作EH⊥AM于H,连接EM.
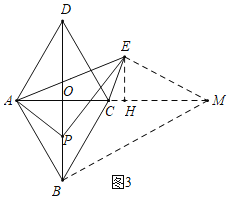
在Rt△ABM中,∵∠ABM=90°,∠BAM=60°,
∴∠AMB=30°,
∴AM=2AB,
在Rt△APE中,∵∠APE=90°,∠PAE=60°,
∴∠AEP=30°,
∴AE=2PA,
∴![]() =
=![]() =2,
=2,
∵∠EAP=∠MAB,
∴∠EAM=∠PAB,
∴△EAM∽△PAB,
∴![]() =
=![]() =2,∠AME=∠ABP=30°,
=2,∠AME=∠ABP=30°,
∴EM=2t,EH=![]() EM=t,
EM=t,
∴S△ACE=![]() ACEH=
ACEH=![]() t(0<t≤6).
t(0<t≤6).

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案