题目内容
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y= (k≠0)的图象经过圆心P,则k= .
(k≠0)的图象经过圆心P,则k= .

﹣ 解:作PD⊥OA于D,PE⊥AB于E,作CH⊥AB于H,如图,设⊙P的半径为r,
解:作PD⊥OA于D,PE⊥AB于E,作CH⊥AB于H,如图,设⊙P的半径为r,
∵⊙P与边AB,AO都相切,
∴PD=PE=r,AD=AE,
在Rt△OAB中,∵OA=8,AB=10,
∴OB= =6,
=6,
∵AC=2,
∴OC=6,
∴△OBC为等腰直角三角形,
∴△PCD为等腰直角三角形,
∴PD=CD=r,
∴AE=AD=2+r,
∵∠CAH=∠BAO,
∴△ACH∽△ABO,
∴ =
= ,即
,即 =
= ,解得CH=
,解得CH= ,
,
∴AH= =
= =
= ,
,
∴BH=10﹣ =
= ,
,
∵PE∥CH,
∴△BEP∽△BHC,
∴ =
= ,即
,即 =
= ,解得r=
,解得r= ,
,
∴OD=OC﹣CD=6﹣ =
= ,
,
∴P( ,﹣
,﹣ ),
),
∴k= ×(﹣
×(﹣ )=﹣
)=﹣ .
.
故答案为﹣ .
.


练习册系列答案
相关题目
荆州素有“鱼米之乡”的美称,某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售,按计划20辆汽车都要装运,每辆汽车只能装运同一种鱼,且必须装满,根据下表提供的信息,解答以下问题:
| 鲢鱼 | 草鱼 | 青鱼 | |
| 每辆汽车载鱼量(吨) | 8 | 6 | 5 |
| 每吨鱼获利(万元) | 0.25 | 0.3 | 0.2 |
(1)设装运鲢鱼的车辆为x辆,装运草鱼的车辆为y辆,求y与x之间的函数关系式;
(2)如果装运每种鱼的车辆都不少于2辆,那么怎样安排车辆能使此次销售获利最大?并求出最大利润.

 的二项式
的二项式 展开式中的常数项是
展开式中的常数项是 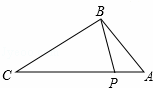
 =
=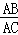 D.
D. 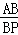 =
=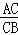


 的解集是______.
的解集是______.