题目内容
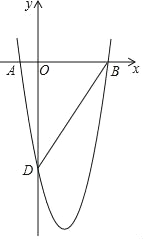
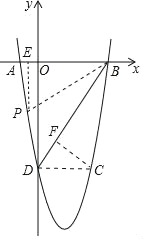
【题目】如图,二次函数y=ax2+bx﹣4![]() 的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
的图象经过A(﹣1,0)、B(4,0)两点,于y轴交于点D.
(1)求这个二次函数的表达式;
(2)已知点C(3,m)在这个二次函数的图象上,连接BC,点P为抛物线上一点,且∠CBP=60°.
①求∠OBD的度数;
②求点P的坐标.
【答案】(1)二次函数的表达式为y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;(2)①60°,②(-
;(2)①60°,②(-![]() ,
,![]() )
)
【解析】分析:(1)代入A、B点坐标即可求得a、b的值,即可解题;
(2)①易证△BOD是含30°角的直角三角形,即可解题;
②过点P作PE⊥x轴于点E,过点C作CF⊥BD于点F,易证△CBF∽△PBE,可得![]() ,即可解题.
,即可解题.
详解:(1)由题意知:![]() ,解得
,解得![]() .
.
∴该二次函数的表达式为y=![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ;
;
(2)①∵当x=0时,y=﹣4![]() .
.
∴抛物线与y轴交点D的坐标为(0,﹣4![]() ).
).
∵在△BOD中,∠BOD=90°,OB=4,OD=4![]() ,
,
∴BD=![]() =8,即BD=2OB,
=8,即BD=2OB,
∴∠ODB=30°.
∴∠OBD=60°;
②过点P作PE⊥x轴于点E,过点C作CF⊥BD于点F,
∵x=3时,m=﹣4![]() .
.
∴点C的坐标为(3,﹣4![]() ).
).
∵CD∥x轴,
∴CD=3,∠CDB=60°,∠DCF=30°.
∴DF=![]() CD=
CD=![]() ,CF=
,CF=![]() ,
,
∵BD=8,
∴BF=8﹣![]() =
=![]() ,
,
设点P的坐标为(x,![]() x2﹣3
x2﹣3![]() x﹣4
x﹣4![]() ).
).
则PE=﹣![]() x2+3
x2+3![]() x+4
x+4![]() ,BE=4﹣x,
,BE=4﹣x,
∵∠CBP=∠OBD=60°,
∴∠CBF=∠PBE.
∵∠CFB=∠PEB=90°.
∴△CBF∽△PBE.
∴![]() .
.
∴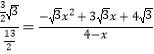 ,
,
解得:x1=4(舍去),x2=﹣![]() .
.
∵当x=﹣![]() 时,y=﹣
时,y=﹣![]() .
.
∴点P的坐标为(﹣![]() ,﹣
,﹣![]() ).
).

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】QQ运动记录的小莉爸爸2017年2月份7天步行的步数(单位:万步)如下表:
日期 | 2月6日 | 2月7日 | 2月8日 | 2月9日 | 2月10日 | 2月11日 | 2月12日 |
步数 | 2.1 | 1.7 | 1.8 | 1.9 | 2.0 | 1.8 | 2.0 |
(1)制作适当的统计图表示小莉爸爸这7天步行的步数的变化趋势;
(2)求小莉爸爸这7天中每天步行的平均步数;
(3)估计小莉爸爸2月份步行的总步数.