题目内容
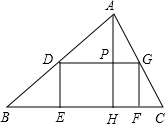
如图,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC,CD于点M,F,BG⊥AC,垂足为C,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=2,求EM的长.

考点:相似三角形的判定与性质;矩形的性质;解直角三角形。
解答:(1)证明:∵四边形ABCD是矩形,
∴∠ABE=∠ECF=90°.
∵AE⊥EF,∠AEB+∠FEC=90°.
∴∠AEB+∠BEA=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF;
(2)△ABH∽△ECM.
证明:∵BG⊥AC,
∴∠ABG+∠BAG=90°,
∴∠ABH=∠ECM,
由(1)知,∠BAH=∠CEM,
∴△ABH∽△ECM;
(3)解:作MR⊥BC,垂足为R,
∵AB=BE=EC=2,
∴AB:BC=MR:RC=2,∠AEB=45°,
∴∠MER=45°,CR=2MR,
∴MR=ER=![]() RC=
RC=![]() ,
,
∴EM=![]() .
.


练习册系列答案
相关题目

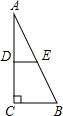 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )