题目内容
已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.(1)如图2,当折叠后的
 经过圆心O时,求
经过圆心O时,求 的长;
的长;(2)如图3,当弦AB=2时,求折叠后
 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离;(3)在图1中,再将纸片⊙O沿弦CD折叠操作.
①如图4,当AB∥CD,折叠后的
 与
与 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;②如图5,当AB与CD不平行,折叠后的
 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.
【答案】分析:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE,可得△OAE、△OBE为等边三角形,从而得到 的圆心角,再根据弧长公式计算即可;
的圆心角,再根据弧长公式计算即可;
(2)如图3,连接O′A、O′B,过点O′作O′E⊥AB于点E,可得△AO′B为等边三角形,根据三角函数的知识可求折叠后 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离;
(3)①如图4, 与
与 所在圆外切于点P时,过点O作EF⊥AB交
所在圆外切于点P时,过点O作EF⊥AB交 于点E,交
于点E,交 于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;
于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;
②根据一组对边平行且相等的四边形是平行四边形即可得证.
解答: 解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE
解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE
∵点E与点O关于AB对称
∴△OAE、△OBE为等边三角形;…1分
∴∠OEA=∠OEB=60°
∴ =
= =
= ;…2分
;…2分
(2)如图3,连接O′A、O′B,
∵ 折叠前后所在的⊙O与⊙O′是等圆,
折叠前后所在的⊙O与⊙O′是等圆,
∴O′A=O′B=OA=AB=2
∴△AO′B为等边三角形;…3分
过点O′作O′E⊥AB于点E
∴O′E=O′B•sin60°= ;…4分
;…4分
(3)①如图4, 与
与 所在圆外切于点P时,
所在圆外切于点P时,
过点O作EF⊥AB交 于点E,交
于点E,交 于点F,
于点F,
∵AB∥CD,
∴EF垂直平分CD、且必过点P,…5分
根据垂径定理及折叠,可知 ,…6分
,…6分
又∵EF=4,
∴点O到AB、CD的距离之和为:
d=PH+PG= ;…7分
;…7分
②如图5,当AB与CD不平行时,
四边形OMPN是平行四边形…8分
 证明如下:
证明如下:
设O′、O″为 和
和 所在圆的圆心,
所在圆的圆心,
由折叠可知:O′与O关于AB对称,O″与O关于CD对称,
∴M为OO′的中点,N为OO″的中点;…9分
∵ 所在圆外切,
所在圆外切,
∴连心线O′O″必过点P,
∵ 所在圆与⊙O都是等圆,
所在圆与⊙O都是等圆,
∴O′P=O″P=2;
∴ ;
;
∴四边形OMPN是平行四边形.
点评:综合考查了相切两圆的性质,等边三角形的判定与性质,平行四边形的判定,垂径定理,弧长的计算,翻折变换(折叠问题),解直角三角形,综合性较强,难度较大.
 的圆心角,再根据弧长公式计算即可;
的圆心角,再根据弧长公式计算即可;(2)如图3,连接O′A、O′B,过点O′作O′E⊥AB于点E,可得△AO′B为等边三角形,根据三角函数的知识可求折叠后
 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离;(3)①如图4,
 与
与 所在圆外切于点P时,过点O作EF⊥AB交
所在圆外切于点P时,过点O作EF⊥AB交 于点E,交
于点E,交 于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;
于点F,根据垂径定理及折叠,可求点O到AB、CD的距离之和;②根据一组对边平行且相等的四边形是平行四边形即可得证.
解答:
 解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE
解:(1)如图2,过点O作OE⊥AB交⊙O于点E,连接OA、OB、AE、BE∵点E与点O关于AB对称
∴△OAE、△OBE为等边三角形;…1分
∴∠OEA=∠OEB=60°
∴
 =
= =
= ;…2分
;…2分(2)如图3,连接O′A、O′B,

∵
 折叠前后所在的⊙O与⊙O′是等圆,
折叠前后所在的⊙O与⊙O′是等圆,∴O′A=O′B=OA=AB=2
∴△AO′B为等边三角形;…3分
过点O′作O′E⊥AB于点E
∴O′E=O′B•sin60°=
 ;…4分
;…4分(3)①如图4,
 与
与 所在圆外切于点P时,
所在圆外切于点P时,
过点O作EF⊥AB交
 于点E,交
于点E,交 于点F,
于点F,∵AB∥CD,
∴EF垂直平分CD、且必过点P,…5分
根据垂径定理及折叠,可知
 ,…6分
,…6分又∵EF=4,
∴点O到AB、CD的距离之和为:
d=PH+PG=
 ;…7分
;…7分②如图5,当AB与CD不平行时,
四边形OMPN是平行四边形…8分
 证明如下:
证明如下:设O′、O″为
 和
和 所在圆的圆心,
所在圆的圆心,由折叠可知:O′与O关于AB对称,O″与O关于CD对称,
∴M为OO′的中点,N为OO″的中点;…9分
∵
 所在圆外切,
所在圆外切,∴连心线O′O″必过点P,
∵
 所在圆与⊙O都是等圆,
所在圆与⊙O都是等圆,∴O′P=O″P=2;
∴
 ;
;∴四边形OMPN是平行四边形.
点评:综合考查了相切两圆的性质,等边三角形的判定与性质,平行四边形的判定,垂径定理,弧长的计算,翻折变换(折叠问题),解直角三角形,综合性较强,难度较大.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目


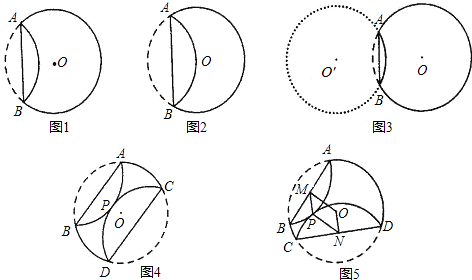
 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;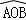 的长度;
的长度; 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;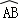 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.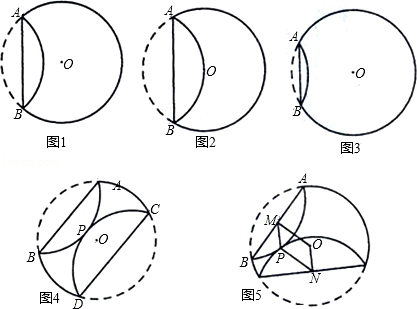
 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;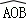 的长度;
的长度; 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;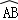 与
与 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.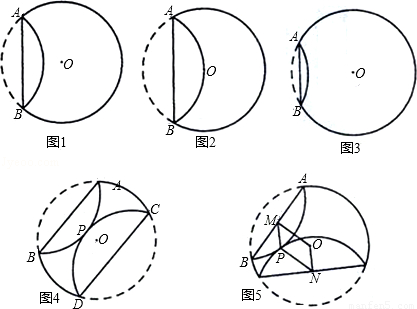
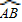 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;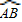 经过圆心为O时,求
经过圆心为O时,求 的长度;
的长度; 与
与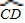 所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB、CD的距离之和为d,求d的值; 与
与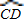 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.