Question

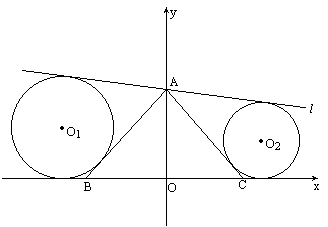
已知：如图，△ABC中，AB＝BC＝CA＝6，BC在x轴上，BC边上的高线AO在y轴上，直线l绕A点转动(与线段BC没有交点)．设与AB、l、x轴相切的⊙O₁的半径为r₁，与AC、l、x轴相切的⊙O₂的半径为r₂．

(1)当直绕l绕点A转动到何位置时，⊙O₁、⊙O₂的面积之和最小，为什么？

(2)若r₁－r₂＝，求图象经过点O₁、O₂的一次函数解析式．

Answer 1

答案：
解析：

解：(1)当l∥x轴时，⊙O1、⊙O2的面积之和最小 　　如图，设切点分别为M、N、D、G，由切线长定理得 　　MN＋DG＝AB＋BC＋AC＝18 　　∵MN＝DG∴DG＝9 　　∴DB＋CG＝3 　　连结O1D、O1B， 　　∴O1D⊥BD，∠DBO1＝，∴DB＝r1 　　同理CG＝r2 　　∴r1＋r2＝3 　　∵⊙O1、⊙O2的面积之和S＝＋π(3－r1)2 　　＝2π[(r1－)2＋]， 　　∴当r1＝r2＝，即l∥x轴时，S最小． 　　(2)由(1)得r1＋r2＝3 　　∵r1－r2＝ 　　∴r1＝2，r2＝ 　　∴O1(－5，2)，O2(4，) 　　设图象经过点O1、O2的一次函数解析式为y＝kx＋b， 　　则 　　解得 　　∴直线O1O2的解析式为y＝－x＋