题目内容
12.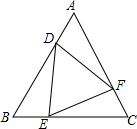 如图,点D、E、F分别是边长为6的等边三角形ABC边AB、BC、AC上的点,且AD=BE=CF.
如图,点D、E、F分别是边长为6的等边三角形ABC边AB、BC、AC上的点,且AD=BE=CF.(1)求证:△DEF是等边三角形;
(2)当AD=2时,求△ADF的面积.
分析 (1)根据等边△ABC中AD=BE=CF,证得△ADF≌△BED≌△CFE即可得出:△DEF是等边三角形;
(2)过F作AB的垂线,垂足为H,可得FH=AF×sin60°=(6-2)×sin60°=2$\sqrt{3}$,${S}_{△ADF}=\frac{1}{2}•AD•AF$可得答案.
解答 (1)证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,
又∵∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是一个等边三角形;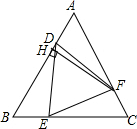
(2)解:过F作AB的垂线,垂足为H,
∵AD=BE=CF=2,
∴FH=AF×sin60°=(6-2)×sin60°=2$\sqrt{3}$,
${S}_{△ADF}=\frac{1}{2}•AD•AF$=$\frac{1}{2}×2×2\sqrt{3}$=2$\sqrt{3}$.
点评 此题主要考查了等边三角形的判定与性质和全等三角形判定及三角形面积公式,根据已知得出△ADF≌△BED≌△CFE是解题关键.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
3.一个不透明的袋子中装有4个红球,2个黄球,这些球除了颜色外都相同,从中随机抽出3个球,下列事件为必然事件的是( )
| A. | 至少有1个球是红球 | B. | 至少有1个球是黄球 | ||
| C. | 至少有2个球是红球 | D. | 至少有2个球是黄球 |
17.下列事件:
(1)抛掷1枚硬币正面朝上;
(2)任意两正整数的和大于1;
(3)打开电视正在播放新闻联播;
(4)长为3cm、5cm、9cm的三条线段能围成一个三角形.
其中确定事件有( )
(1)抛掷1枚硬币正面朝上;
(2)任意两正整数的和大于1;
(3)打开电视正在播放新闻联播;
(4)长为3cm、5cm、9cm的三条线段能围成一个三角形.
其中确定事件有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.若多项式4x2+mx+1是完全平方式,则m的值是( )
| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
1.下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )
| A. | a=$\sqrt{5}$ b=2 c=3 | B. | a=7 b=24 c=5 | C. | a=6 b=8 c=10 | D. | a=3 b=4 c=5 |
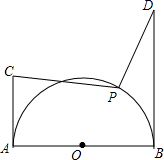 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.
如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值. 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.