题目内容
如图，AM∥BC，∠M=∠C，求证：∠1=∠2．
证明：∵AM∥BC，
∴∠M=∠BDM，
∵∠M=∠C，
∴∠BDM=∠C，
∴AC∥MD，
∴∠1=∠2．
分析：由AM∥BC，根据平行线的性质，可证得∠M=∠BDM，又由∠M=∠C，可证得∠BDM=∠C，根据平行线的判定，可证得MD∥AC，继而证得结论．
点评：此题考查了平行线的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
∴∠M=∠BDM，
∵∠M=∠C，
∴∠BDM=∠C，
∴AC∥MD，
∴∠1=∠2．
分析：由AM∥BC，根据平行线的性质，可证得∠M=∠BDM，又由∠M=∠C，可证得∠BDM=∠C，根据平行线的判定，可证得MD∥AC，继而证得结论．
点评：此题考查了平行线的判定与性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
阅读快车系列答案
相关题目
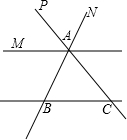
如图，AM∥BC，直线AB交AM于A，交BC于B，且∠ABC≠60°，AP是∠MAN的平分线，AP的反向延长线交BC于C，那么这个图形中共有相等的角（小于平角的角）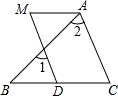
如图，AM∥BC，∠M=∠C，求证：∠1=∠2．
